题目内容
如图,二面角 的大小是60°线段
的大小是60°线段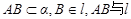 所成的角
所成的角
为30°,则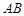 与平面
与平面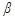 所成的角的正弦值是___________.
所成的角的正弦值是___________.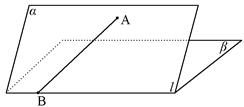
【答案】
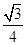
【解析】
试题分析:过点A作平面β的垂线,垂足为C,
在β内过C作l的垂线.垂足为D
连接AD,有三垂线定理可知AD⊥l,
故∠ADC为二面角α-l-β的平面角,为60°
又由已知,∠ABD=30°
连接CB,则∠ABC为AB与平面β所成的角
设AD=2,则AC=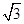 ,CD=1
,CD=1
AB=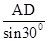 =4
=4
∴sin∠ABC=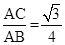 ;
;
故答案为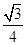 .
.
考点:本题主要考查了平面与平面之间的位置关系,以及直线与平面所成角、二面角的计算问题。
点评:典型题,通过“一作、二证、三算”,明确∠ABC为AB与平面β所成的角,在直角三角形ABC中求出此角即可.

练习册系列答案
相关题目
 如图,二面角
如图,二面角 的大小是60°,线段
的大小是60°,线段 ,AB与
,AB与 所成角为30°,则AB与平面
所成角为30°,则AB与平面 所成的角的正弦值是________________。
所成的角的正弦值是________________。
 的大小是60°,线段
的大小是60°,线段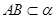 .
.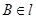 ,
, 与
与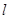 所成的角为30°.则
所成的角为30°.则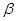 所成的角的正弦值是 .
所成的角的正弦值是 .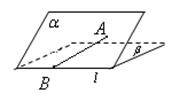
 的大小是60°,线段
的大小是60°,线段 .
. ,
, 与
与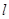 所成的角为30°.则
所成的角为30°.则 所成的角的正弦值是
.
所成的角的正弦值是
.