题目内容
数列{an}是以a1=4为首项的等比数列,且S3,S2,S4成等差数列.(1)求{an}的通项公式;
(2)设bn=log2|an|,Tn为数列{
| 1 | bn•bn+1 |
分析:(1)讨论q是否为1,然后根据S3,S2,S4成等差数列建立等式关系,求出公比q,从而求出{an}的通项公式;
(2)先求出bn,然后将
分解成
-
,最后求和即可得到答案.
(2)先求出bn,然后将
| 1 |
| bn•bn+1 |
| 1 |
| n+1 |
| 1 |
| n+2 |
解答:解:(1)q=1时,显然不成立;
q≠1时,∵S3,S2,S4成等差数列
∴S3+S4=2S2则2a3+a4=0
∴q=-2
∴an=(-2)n+1
(2)bn=log2|an|=n+1
∴
=
-
Tn=
-
+
-
+…+
-
=
-
q≠1时,∵S3,S2,S4成等差数列
∴S3+S4=2S2则2a3+a4=0
∴q=-2
∴an=(-2)n+1
(2)bn=log2|an|=n+1
∴
| 1 |
| bn•bn+1 |
| 1 |
| n+1 |
| 1 |
| n+2 |
Tn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2 |
| 1 |
| n+2 |
点评:本题主要考查了等比数列的通项以及利用裂项求和法求数列的前n项和,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设数列{an}是以2为首项,1为公差的等差数列,{bn}是以1为首项,2为公比的等比数列,则b a1+b a2+…+b a6等于( )
| A、78 | B、84 | C、124 | D、126 |
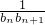 }的前n项的和,求Tn.
}的前n项的和,求Tn. }的前n项的和,求Tn.
}的前n项的和,求Tn.