题目内容
已知:A,B,C是直线l上的点,O是直线l外一点,且
-[f(x)+
]
+x3
=
,若当x∈[-1,1]时,af(x)-3x+1≥0恒成立,则实数a的值为______.
| OA |
| f(1) |
| 3 |
| OB |
| OC |
| 0 |
∵A,B,C是直线l上的点,O是直线l外一点,且
-[f(x)+
]
+x3
=
,
∴f(x)+
-x3=0,
∴f(1)+
-1=0,
∴f(1)=
,
∴f(x)=x3-
,
∴af(x)-3x+1≥0为a(x3-
)-3x+1≥0
(1)a=0时,-3x+1≥0在[-1,1]上不能恒成立
(2)a<0时,f′(x)=3ax2-3<0,f(x)是减函数,其最小值为f(1).
若对x∈[-1,1],f(x)≥0恒成立,则需f(1)≥0
即
a-3+1≥0,
∴a≥
,
∵a<0,∴此时无解.
(3)a>0时,f(x)=a(x3-
)-3x+1≥0恒成立,x∈[-1,1],
①x=0时,-
+1≥0成立,∴a≥4
②0<x≤1时,a≥
令g(x)=
,求导得g′(x)=
易知0<x<
时函数递增,
<x<1时递减,
∴g(x)最大值为g(
)=4,
∴a≥4
③-1≤x<0时,a≤
令g(x)=
,求导得g′(x)=
可知g(x)在-1<x<0时是增函数,其最小值为g(-1)=4
∴a≤4
由②知a≥4,
∴a=4.
综上知a=4.
| OA |
| f(1) |
| 3 |
| OB |
| OC |
| 0 |
∴f(x)+
| f(1) |
| 3 |
∴f(1)+
| f(1) |
| 3 |
∴f(1)=
| 3 |
| 4 |
∴f(x)=x3-
| 1 |
| 4 |
∴af(x)-3x+1≥0为a(x3-
| 1 |
| 4 |
(1)a=0时,-3x+1≥0在[-1,1]上不能恒成立
(2)a<0时,f′(x)=3ax2-3<0,f(x)是减函数,其最小值为f(1).
若对x∈[-1,1],f(x)≥0恒成立,则需f(1)≥0
即
| 3 |
| 4 |
∴a≥
| 8 |
| 3 |
∵a<0,∴此时无解.
(3)a>0时,f(x)=a(x3-
| 1 |
| 4 |
①x=0时,-
| a |
| 4 |
②0<x≤1时,a≥
| 3x-1 |
| x3 |
令g(x)=
| 3x-1 |
| x3 |
| -6x+3 |
| x4 |
易知0<x<
| 1 |
| 2 |
| 1 |
| 2 |
∴g(x)最大值为g(
| 1 |
| 2 |
∴a≥4
③-1≤x<0时,a≤
| 3x-1 |
| x3 |
令g(x)=
| 3x-1 |
| x3 |
| -6x+3 |
| x4 |
可知g(x)在-1<x<0时是增函数,其最小值为g(-1)=4
∴a≤4
由②知a≥4,
∴a=4.
综上知a=4.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目






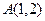 ,点
,点 ,若
,若 ,则点
,则点 的坐标是 。
的坐标是 。