题目内容
若抛物线 的焦点是
的焦点是 ,准线是
,准线是 ,则经过点
,则经过点 、
、 (4,4)且与
(4,4)且与 相切的圆共有
相切的圆共有
A. 个 个 | B. 个 个 | C. 个 个 | D. 个 个 |
C
解析考点:抛物线的简单性质;直线与圆的位置关系.
分析:根据抛物线的方程求得焦点坐标和准线的方程,设出所求圆的圆心,表示出半径,则圆的方程可得,把M,F点的坐标代入整理求得h,和g,则圆的方程可得.
解:抛物线y2=4x的焦参数p=2,所以F(1,0),直线l:x=-1,即x+1=0,
设经过点M(4,4)、F(1,0),且与直线l相切的圆的圆心为Q(g,h),
则半径为Q到,l的距离,即1+g,所以圆的方程为(x-g)2+(y-h)2=(1+g)2,
将M、F的坐标代入,得(4-g)2+(4-h)2=(1+g)2,(1-g)2+(0-h)2=(1+g)2,
即h2-8h+1=10g①,
h2=4g②,②代入①,
得3h2+16h-2=0,
解得h1= ,h2=-
,h2=- ,(经检验无增根)
,(经检验无增根)
代入②得g1= ,g2=
,g2= ,
,
所以满足条件的圆有两个:
(x- )2+(y-
)2+(y- )2=(
)2=( )2,
)2,
(x- )2+(y+
)2+(y+ )2=(
)2=(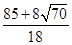 )2.
)2.
故选C

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
顶点在原点,且过点 的抛物线的标准方程是( )
的抛物线的标准方程是( )
A. | B. |
C. 或 或 | D. 或 或 |
椭圆 的离心率等于( ).
的离心率等于( ).
A. | B. | C.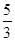 | D. |
设定点 与抛物线
与抛物线 上的点
上的点 的距离为
的距离为 ,
, 到抛物线焦点F的距离为
到抛物线焦点F的距离为 ,则
,则 取最小值时,
取最小值时, 点的坐标为( ).
点的坐标为( ).
A. | B. | C. | D.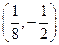 |
双曲线 (
( )的渐近线上任意一点P到两个焦点的距离之差的绝对值与
)的渐近线上任意一点P到两个焦点的距离之差的绝对值与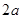 的大小关系为
的大小关系为
A.恒等于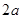 | B.恒大于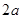 | C.恒小于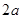 | D.不确定 |
已知双曲线 的一条渐近线方程为
的一条渐近线方程为 ,则此双曲线的离心率为
,则此双曲线的离心率为
A. | B. | C.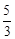 | D.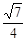 |
若点 的坐标是
的坐标是 ,F是抛物线
,F是抛物线 的焦点,点
的焦点,点 在抛物线上移动,为使得
在抛物线上移动,为使得 取得最小值,则
取得最小值,则 点的坐标是
点的坐标是 ( )
( )
A. | B. | C. | D.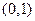 |
已知两点 和
和 ,若曲线上存在点P,使
,若曲线上存在点P,使 ,则称该曲线为“Q型曲线”. 给出下列曲线:①
,则称该曲线为“Q型曲线”. 给出下列曲线:① ;②
;② ;③
;③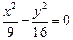 ;④
;④ ,其中为“Q型曲线”的是 ( )
,其中为“Q型曲线”的是 ( )
| A.①和② | B.②和③ | C.①和④ | D.②和④ |
 分别是双曲线
分别是双曲线 的中心和左焦点,点P为双曲线右支上的任意一点,则
的中心和左焦点,点P为双曲线右支上的任意一点,则 的取值范围为 ( )
的取值范围为 ( )


