题目内容
(本题满分12分)
已知函数f(x)= +2sin2x
+2sin2x
(1)求函数f(x)的最大值及此时x的值;
(2)求函数f(x)的单调递减区间。
已知函数f(x)=
 +2sin2x
+2sin2x(1)求函数f(x)的最大值及此时x的值;
(2)求函数f(x)的单调递减区间。
x=kπ+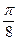 (k∈Z)时,f(x)取得最大值2
(k∈Z)时,f(x)取得最大值2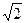 -1,[kπ+
-1,[kπ+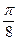 ,kπ+
,kπ+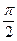 ,(kπ+
,(kπ+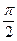 ,kπ+
,kπ+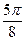
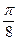 (k∈Z)时,f(x)取得最大值2
(k∈Z)时,f(x)取得最大值2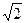 -1,[kπ+
-1,[kπ+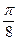 ,kπ+
,kπ+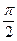 ,(kπ+
,(kπ+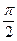 ,kπ+
,kπ+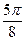
解:(1)∵cos3x=4cos3x-3cosx,则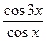 =4cos2x-3=2cos2x-1
=4cos2x-3=2cos2x-1
∴f(x)=2cos2x-1+2sin2x
=2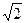 sin(2x+
sin(2x+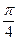 )-1 ……………………4分
)-1 ……………………4分
在2x+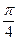 =2kπ+
=2kπ+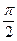 时,f(x)取得最大值2
时,f(x)取得最大值2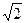 -1
-1
即在x=kπ+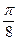 (k∈Z)时,f(x)取得最大值2
(k∈Z)时,f(x)取得最大值2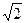 -1 ……………………6分
-1 ……………………6分
(2)∵f(x)=2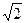 sin(2x+
sin(2x+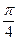 )-1
)-1
要使f(x)递减,x满足2kπ+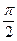 ≤2x+
≤2x+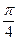 ≤2kπ+
≤2kπ+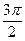
即kπ+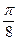 ≤x≤kπ+
≤x≤kπ+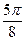 (k∈Z)
(k∈Z)
又∵cosx≠0,即x≠kπ+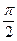 (k∈Z) ……………………10分
(k∈Z) ……………………10分
于是[kπ+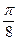 ,kπ+
,kπ+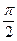 ,(kπ+
,(kπ+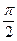 ,kπ+
,kπ+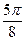 均为减区间 …………12分
均为减区间 …………12分
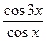 =4cos2x-3=2cos2x-1
=4cos2x-3=2cos2x-1∴f(x)=2cos2x-1+2sin2x
=2
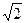 sin(2x+
sin(2x+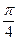 )-1 ……………………4分
)-1 ……………………4分在2x+
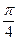 =2kπ+
=2kπ+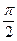 时,f(x)取得最大值2
时,f(x)取得最大值2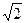 -1
-1即在x=kπ+
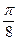 (k∈Z)时,f(x)取得最大值2
(k∈Z)时,f(x)取得最大值2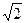 -1 ……………………6分
-1 ……………………6分(2)∵f(x)=2
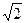 sin(2x+
sin(2x+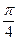 )-1
)-1要使f(x)递减,x满足2kπ+
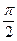 ≤2x+
≤2x+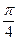 ≤2kπ+
≤2kπ+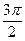
即kπ+
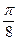 ≤x≤kπ+
≤x≤kπ+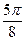 (k∈Z)
(k∈Z)又∵cosx≠0,即x≠kπ+
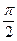 (k∈Z) ……………………10分
(k∈Z) ……………………10分
|
|
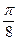 ,kπ+
,kπ+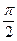 ,(kπ+
,(kπ+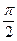 ,kπ+
,kπ+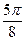 均为减区间 …………12分
均为减区间 …………12分
练习册系列答案
相关题目
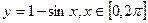 的图象的作法。
的图象的作法。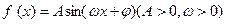 的图象
的图象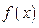 = ;
= ;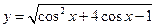 的最大值和最小值.
的最大值和最小值.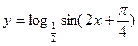 的单调减区间为 ( )
的单调减区间为 ( )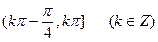
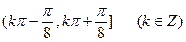
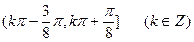
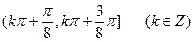
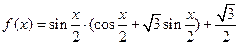 .(1) 求函数
.(1) 求函数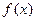 的最小正周期,并写出函数
的最小正周期,并写出函数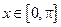 ,求函数
,求函数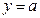 (
(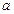 为常数)与
为常数)与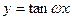
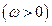 的相邻两支的交点距离为 ( )
的相邻两支的交点距离为 ( )


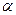 ,β都是第二象限的角,且sin
,β都是第二象限的角,且sin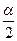 <tan
<tan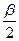
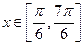 时,函数
时,函数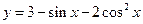 的最小值是_______,最大值是________。
的最小值是_______,最大值是________。