题目内容
关于函数 ,有以下命题
,有以下命题(1)
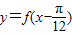 为偶函数;
为偶函数; (2)y=f(x)的图象关于直线
 对称;
对称;(3)函数f(x)在区间
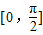 的值域为
的值域为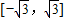 ;
;(4)y=f(x)在
 的减区间是
的减区间是 和
和 .
.其中正确命题的序号为 .
【答案】分析:把函数 中的x替换为
中的x替换为 ,化简整理后即可判断函数
,化简整理后即可判断函数 的奇偶性;
的奇偶性;
把 代入函数解析式,根据函数能否取得最值判断y=f(x)的图象是否关于直线
代入函数解析式,根据函数能否取得最值判断y=f(x)的图象是否关于直线 对称;
对称;
直接由x∈ ,求解函数
,求解函数 的值域,从而能判断命题(3)的真假;
的值域,从而能判断命题(3)的真假;
根据复合函数的单调性,求解函数 的单调区间,然后根据k的取值,求得函数f(x)在
的单调区间,然后根据k的取值,求得函数f(x)在 上的减区间.由以上分析即可得到正确答案.
上的减区间.由以上分析即可得到正确答案.
解答:解:由 ,得:y=
,得:y= =
= ,
,
函数的定义域为R,且-2cos2(-x)=-2cos2x,∴函数 为偶函数,∴命题(1)正确;
为偶函数,∴命题(1)正确;
把 代入
代入 ,得:
,得: ,
,
∴y=f(x)的图象关于直线 对称,∴命题(2)正确;
对称,∴命题(2)正确;
由 ,得:
,得: ,∴
,∴ ,
,
∴函数f(x)在区间 的值域为[-1,2],∴命题(3)错误;
的值域为[-1,2],∴命题(3)错误;
由 (k∈Z),得:
(k∈Z),得: (k∈Z),
(k∈Z),
取k=-1,得: ,取k=0,得:
,取k=0,得: .
.
∴y=f(x)在 的减区间是
的减区间是 和
和 ,∴命题(4)正确.
,∴命题(4)正确.
所以,正确的命题为(1)(2)(4).
故答案为(1)(2)(4).
点评:本题考查了判断命题真假,比较综合的考查了三角函数的一些性质,解答此题的关键是对三角函数的性质的理解与掌握,若能借助于单位圆中的三角函数线处理该题,将会使问题简洁化,此题属中档题.
 中的x替换为
中的x替换为 ,化简整理后即可判断函数
,化简整理后即可判断函数 的奇偶性;
的奇偶性;把
 代入函数解析式,根据函数能否取得最值判断y=f(x)的图象是否关于直线
代入函数解析式,根据函数能否取得最值判断y=f(x)的图象是否关于直线 对称;
对称;直接由x∈
 ,求解函数
,求解函数 的值域,从而能判断命题(3)的真假;
的值域,从而能判断命题(3)的真假;根据复合函数的单调性,求解函数
 的单调区间,然后根据k的取值,求得函数f(x)在
的单调区间,然后根据k的取值,求得函数f(x)在 上的减区间.由以上分析即可得到正确答案.
上的减区间.由以上分析即可得到正确答案.解答:解:由
 ,得:y=
,得:y= =
= ,
,函数的定义域为R,且-2cos2(-x)=-2cos2x,∴函数
 为偶函数,∴命题(1)正确;
为偶函数,∴命题(1)正确;把
 代入
代入 ,得:
,得: ,
,∴y=f(x)的图象关于直线
 对称,∴命题(2)正确;
对称,∴命题(2)正确;由
 ,得:
,得: ,∴
,∴ ,
,∴函数f(x)在区间
 的值域为[-1,2],∴命题(3)错误;
的值域为[-1,2],∴命题(3)错误;由
 (k∈Z),得:
(k∈Z),得: (k∈Z),
(k∈Z),取k=-1,得:
 ,取k=0,得:
,取k=0,得: .
.∴y=f(x)在
 的减区间是
的减区间是 和
和 ,∴命题(4)正确.
,∴命题(4)正确.所以,正确的命题为(1)(2)(4).
故答案为(1)(2)(4).
点评:本题考查了判断命题真假,比较综合的考查了三角函数的一些性质,解答此题的关键是对三角函数的性质的理解与掌握,若能借助于单位圆中的三角函数线处理该题,将会使问题简洁化,此题属中档题.

练习册系列答案
相关题目
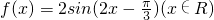 ,有以下命题
,有以下命题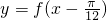 为偶函数;
为偶函数; 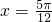 对称;
对称; 的值域为
的值域为 ;
; 的减区间是
的减区间是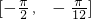 和
和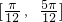 .
. ,有以下命题
,有以下命题 为偶函数;
为偶函数; 的图象关于直线
的图象关于直线 对称;
对称;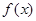 在区间
在区间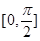 的值域为
的值域为 ;
; 的减区间是
的减区间是 和
和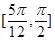 .
.