题目内容
下列关于函数f(x)=(2x-x2)ex的判断正确的是( )① f(x)>0的解集是{x|0<x<2}.
② f(-![]() )是极小值,f(
)是极小值,f(![]() )是极大值.
)是极大值.
③ f(x)没有最小值,也没有最大值.
④ f(x)有最大值,没有最小值.
A.① ③ B.① ② ③ C.② ④ D.① ② ④
D
解析:本题考查不等式的解法以及函数最值、极值的求法,注意倒数的应用.对①有:f(x)=(2x-x2)ex>0![]() 2x-x2>0
2x-x2>0![]() 0<x<2.对②③有:
0<x<2.对②③有:![]() (x)=(2-2x)ex+(2x-x2)ex=(2-x2)ex,令
(x)=(2-2x)ex+(2x-x2)ex=(2-x2)ex,令![]() (x)=0可得:x=±
(x)=0可得:x=±![]() .
.
列出x、![]() (x)、f(x)的变化趋势表:
(x)、f(x)的变化趋势表:
x | (-∞,- | - | (- |
| ( |
| - | 0 | + | 0 | - |
f(x) | □ | 极大值 | □ | 极小值 | □ |
由表可得函数f(x)=(2x-x2)ex>0的草图为:
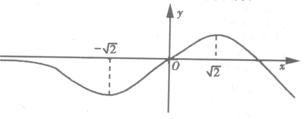
从图中可以看出:f(-![]() )是极小值,f(
)是极小值,f(![]() )为极大值;函数有最大值f(
)为极大值;函数有最大值f(![]() )而无最小值.故选D.
)而无最小值.故选D.

练习册系列答案
相关题目
下列关于函数f(x)=2sin(2x-
)+1的命题正确的是( )
| π |
| 3 |
A、函数f(x)在区间(-
| ||||
B、函数f(x)的对称轴方程是x=
| ||||
C、函数f(x)的对称中心是(kπ+
| ||||
D、函数f(x)可以由函数g(x)=2cos2x+1向右平移
|
 <x≤m+
<x≤m+ (k∈Z)对称;
(k∈Z)对称;