题目内容
已知集合A={y|y=lg(x-3)},B={a|a2-a+3>0},则“x>4”是“A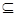 B”的
B”的
| A.充分而不必要条件 |
| B.必要而不充分条件 |
| C.充分必要条件 |
| D.既不充分也不必要条件 |
A
解析∵x>4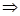 lg(x-3)>0即A为正数集合
lg(x-3)>0即A为正数集合
又∵△=(-1)2-4×1×3=-11<0∴B=R
所以A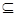 B,即“x>4”是“A
B,即“x>4”是“A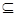 B”的充分条件
B”的充分条件
反之,若A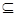 B,则x>3,即必要性不成立
B,则x>3,即必要性不成立
所以“x>4”是“A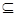 B”的充分不必要条件
B”的充分不必要条件

练习册系列答案
相关题目
集合P={x|2kπ≤α≤(2k+1)π,k∈Z},Q={α|-4≤α≤4}.则P∩Q=( )
A.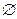 |
| B.{α|-4≤α≤-π或0≤α≤π} |
| C.{α|-4≤α≤4} |
| D.{α|0≤α≤π} |
设集合 ,
, ,i为虚数单位,
,i为虚数单位, ,则M∩N为( )
,则M∩N为( )
| A.(0,1) | B.(0,1] | C.[0,1) | D.[0,1] |
已知集合A={x|4≤ ≤16},B=[a,b],若A⊆B,则实数a-b的取值范围是( )
≤16},B=[a,b],若A⊆B,则实数a-b的取值范围是( )
| A.(-∞,-2] | B. | C.(-∞,2] | D. |
设集合M= ,N=
,N=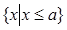 ,若
,若 ,则
,则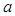 的取值范围是 ( )
的取值范围是 ( )
A.(? ,1) ,1) | B.(?∞,1] | C.[1,+∞) | D.(2,+∞) |
设全集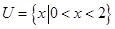 ,集合
,集合 ,则集合
,则集合 ( )
( )
A.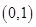 | B. | C.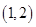 | D.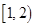 |
设集合A={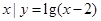 },B={
},B={ },则
},则
| A.(2,+∞) | B.[2,+∞) | C.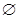 | D.R |
已知集合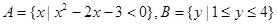 ,则下列结论正确的是( )
,则下列结论正确的是( )
A.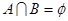 |
B.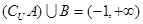 |
C. |
D.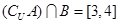 |