题目内容
函数f：R→R，对任意的实数x，y，只要x+y≠0，就有f（xy）=
成立，则函数f（x）（x∈R）的奇偶性为（ ）A．奇函数
B．偶函数
C．既是奇函数又是偶函数
D．既不是奇函数又不是偶函数
【答案】分析：根据x，y的任意性，对函数进行赋值，x=1，y=0得到f（1）=0，再令y=1得f（x），根据奇偶性的定义判断即可．
解答：解：∵对任意的实数x，y，只要x+y≠0，就有f（xy）=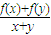
成立
∴令x=1，y=0等式成立，即f（0）=f（1）+f（0）
∴f（1）=0
另可令y=1，x∈R
∴f（x）=
即
对?x∈R恒成立
∴f（x）≡0
即f（x）既是奇函数又是偶函数
故选C
点评：本题考查抽象函数的奇偶性，解题的关键是合理进行赋值，利用函数奇偶性的定义解决，属于基础题．
解答：解：∵对任意的实数x，y，只要x+y≠0，就有f（xy）=
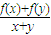成立∴令x=1，y=0等式成立，即f（0）=f（1）+f（0）
∴f（1）=0
另可令y=1，x∈R
∴f（x）=
即
对?x∈R恒成立∴f（x）≡0
即f（x）既是奇函数又是偶函数
故选C
点评：本题考查抽象函数的奇偶性，解题的关键是合理进行赋值，利用函数奇偶性的定义解决，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
相关题目