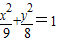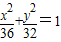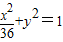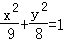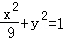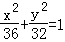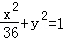题目内容
椭圆长轴上的两端点A1(-3,0),A2(3,0),两焦点恰好把长轴三等分,则该椭圆的标准方程为
- A.
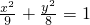
- B.

- C.
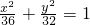
- D.
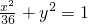
A
分析:由题意可设所求的椭圆的方程为 ,且a=3,再由两焦点恰好把长轴三等分可得a=3c,从而可求c,然后根据
,且a=3,再由两焦点恰好把长轴三等分可得a=3c,从而可求c,然后根据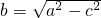 可求b的值,进而可求椭圆的方程.
可求b的值,进而可求椭圆的方程.
解答:由题意可设所求的椭圆的方程为 ,且a=3
,且a=3
由两焦点恰好把长轴三等分可得2a=6c即a=3c=3
c=1,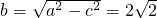
故所求的椭圆方程为: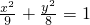
故选A.
点评:对于椭圆方程的求解一般需要先判断椭圆的焦点位置,进而设出椭圆的方程,求解出a,b的值.
分析:由题意可设所求的椭圆的方程为
 ,且a=3,再由两焦点恰好把长轴三等分可得a=3c,从而可求c,然后根据
,且a=3,再由两焦点恰好把长轴三等分可得a=3c,从而可求c,然后根据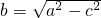 可求b的值,进而可求椭圆的方程.
可求b的值,进而可求椭圆的方程.解答:由题意可设所求的椭圆的方程为
 ,且a=3
,且a=3由两焦点恰好把长轴三等分可得2a=6c即a=3c=3
c=1,
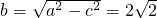
故所求的椭圆方程为:
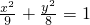
故选A.
点评:对于椭圆方程的求解一般需要先判断椭圆的焦点位置,进而设出椭圆的方程,求解出a,b的值.

练习册系列答案
相关题目
椭圆长轴上的两端点A1(-3,0),A2(3,0),两焦点恰好把长轴三等分,则该椭圆的标准方程为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|