题目内容
 (从以下三题中选做两题,如有多选,按得分最低的两题记分.)
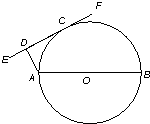
(从以下三题中选做两题,如有多选,按得分最低的两题记分.)(A)AB是圆O的直径,EF切圆O于C,AD⊥EF于D,AD=2,AB=6,则AC长为
(B)若不等式|x-2|+|x+3|<a的解集为∅,则a的取值范围为
(C)参数方程
|
分析:(A)延长BA交EF于点M,由直角三角形相似求得MA,利用直角三角形中的边角关系求出cos∠COA,余弦定理求出 AC.
(B)|x-2|+|x+3|最小值为5,不等式|x-2|+|x+3|<a的解集为∅,故 a<5.
(C)参数方程
(α是参数)化为普通方程为 y=3-
,|x|≤2
(B)|x-2|+|x+3|最小值为5,不等式|x-2|+|x+3|<a的解集为∅,故 a<5.
(C)参数方程
|
| x2 |
| 2 |
解答:解:(A)延长BA交EF于点M,由于直角三角形MAD和直角三角形 MOC相似,∴
=
,
∴
=
,∴MA=6,cos∠COA=cos∠DAM=
=
=
.
由余弦定理可得 AC=
=2
,故答案为 2
.
(B)|x-2|+|x+3|表示数轴上的x对应点到-3和2对应点距离之和,最小值为5,不等式|x-2|+|x+3|<a的解集为∅,
故 a<5,故答案为 (-∞,5].
(C)参数方程
(α是参数)化为普通方程为 y=3-
,|x|≤2,故答案为 y=3-
,
|x|≤2,
| AD |
| OC |
| MA |
| MO |
∴
| 2 |
| 3 |
| MA |
| MA+3 |
| AD |
| MA |
| 2 |
| 6 |
| 1 |
| 3 |
由余弦定理可得 AC=
| 9+9-2×3×3cos∠COA |
| 3 |
| 3 |
(B)|x-2|+|x+3|表示数轴上的x对应点到-3和2对应点距离之和,最小值为5,不等式|x-2|+|x+3|<a的解集为∅,
故 a<5,故答案为 (-∞,5].
(C)参数方程
|
| x2 |
| 2 |
| x2 |
| 2 |
|x|≤2,
点评:本题考查把参数方程化为普通方程的方法,余弦定理,绝对值不等式的解法,(A)中求出cos∠COA 的值,是解题的关键.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目

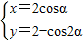 (α是参数)表示的曲线的普通方程是 .
(α是参数)表示的曲线的普通方程是 .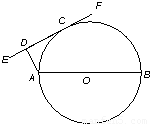
 ,若关于
,若关于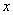 的方程
的方程 有实根,则
有实根,则 的取值范围是 .
的取值范围是 . 、
、 的极坐标方程分别为
的极坐标方程分别为 ,
,
 ,则曲线
,则曲线