题目内容
选修4-4:极坐标系与参数方程
已知曲线C1:
(t为参数),C2:
(θ为参数).
(1)化C1,C2的方程为普通方程;
(2)若C1上的点P对应的参数为t=
,Q为C2上的动点,求PQ中点M到直线C3:
(t为参数)距离的最小值.
已知曲线C1:
|
|
(1)化C1,C2的方程为普通方程;
(2)若C1上的点P对应的参数为t=
| π |
| 2 |
|
分析:(1)把所给的参数方程利用同角三角函数的基本关系消去参数,化为普通方程.
(2)设Q(8cosθ,3sinθ),由中点公式求得M的坐标,根据点M到直线C3 的距离为 d=
=
,可得当sin(θ+∅)=1时,d取得最小值.
(2)设Q(8cosθ,3sinθ),由中点公式求得M的坐标,根据点M到直线C3 的距离为 d=
| |4cosθ-2-(4+3sinθ)-7| | ||
|
| |5sin(θ+∅)-13| | ||
|
解答:解:(1)对于曲线C1:
(t为参数),利用同角三角函数的基本关系消去参数t,可得 (x+4)2+(y-3)2=1;
对于曲线 C2:
(θ为参数),利用同角三角函数的基本关系消去参数θ,可得
+
=1.
(2)若C1上的点P对应的参数为t=
,则点P的坐标为(-4,4),
设Q(8cosθ,3sinθ)为C2上的动点,则PQ中点M( 4cosθ-2,
).
直线C3:
(t为参数),即 x-2y-7=0.
∴点M到直线C3:x-2y-7=0 的距离为 d=
=
=
,其中,sin∅=
,cos∅=-
.
故当sin(θ+∅)=1时,d取得最小值为
=
.
|
对于曲线 C2:
|
| x2 |
| 64 |
| y2 |
| 9 |
(2)若C1上的点P对应的参数为t=
| π |
| 2 |
设Q(8cosθ,3sinθ)为C2上的动点,则PQ中点M( 4cosθ-2,
| 4+3sinθ |
| 2 |
直线C3:
|
∴点M到直线C3:x-2y-7=0 的距离为 d=
| |4cosθ-2-(4+3sinθ)-7| | ||
|
| |4cosθ-3sinθ-13| | ||
|
| |5sin(θ+∅)-13| | ||
|
| 4 |
| 5 |
| 3 |
| 5 |
故当sin(θ+∅)=1时,d取得最小值为
| |5-13| | ||
|
8
| ||
| 5 |
点评:本题主要考查把参数方程化为普通方程的方法,中点公式、点到直线的距离公式的应用,辅助角公式、正弦函数的最值,属于中档题.

练习册系列答案
相关题目
 的参数方程为
的参数方程为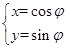 (
(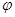 为参数),以坐标原点
为参数),以坐标原点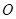 为极点,
为极点,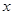 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆 的极坐标方程为
的极坐标方程为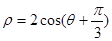 .
.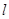 的方程为x-y+4=0,曲线C的参数方程为
的方程为x-y+4=0,曲线C的参数方程为
 ,判断点P与直线
,判断点P与直线