题目内容
对实数a和b,定义新运算a⊙b=
,设函数f(x)=(x2-2)⊙(2x-x2),x∈R.若关于x的方程f(x)=m恰有两个实数解,则实数m的取值范围是
|
m<-3,或m=-2,或-1<m<0
m<-3,或m=-2,或-1<m<0
.分析:根据定义的运算法则化简函数f(x)=(x2-2)⊙(2x-x2)的解析式,并画出f(x)的图象,关于x的方程f(x)=m恰有两个实数解,转化为y=f(x),y=m图象的交点问题,结合图象求得实数m的取值范围.
解答:解:∵a⊙b=
,
∴(x2-2)-(2x-x2)≤2解得-1≤x≤2,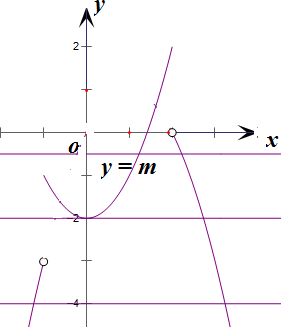
∴f(x)=(x2-2)⊙(2x-x2)=
,
画出函数f(x)的图象,与y=m的图象,如右图,
从而可得:m<-3,或m=-2,或-1<m<0,
故答案为:m<-3,或m=-2,或-1<m<0.
|
∴(x2-2)-(2x-x2)≤2解得-1≤x≤2,
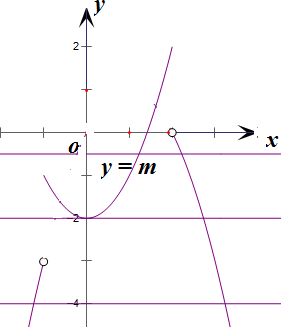
∴f(x)=(x2-2)⊙(2x-x2)=
|
画出函数f(x)的图象,与y=m的图象,如右图,
从而可得:m<-3,或m=-2,或-1<m<0,
故答案为:m<-3,或m=-2,或-1<m<0.
点评:本小题主要考查函数的零点与方程根的关系、不等式的解法等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于中档题.

练习册系列答案
相关题目