题目内容
设等差数列｛an｝的前n项和为Sn，且S4=4S2，a2n=2an+1
（1） 求数列｛an｝的通项公式；
（2） 设数列｛bn｝的前n项和Tn，且Tn+
= λ（λ为常数），令cn=b2n，（n∈N•）.求数列｛cn｝的前n项和Rn.
解答：（1）由S4=4S2，a2n=2an+1，｛an｝为等差数列，可得，
所以
（2）由Tn+ = λ可得，
，Tn-1+
= λ两式相减可得，当
时，
，所以当
时，cn=b2n=
，错位相减法可得，Rn=
当
时，cn=b2n=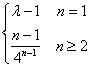
，可得Rn=
练习册系列答案
阅读快车系列答案
相关题目