题目内容
如果集合M={y|y=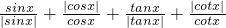 ,x
,x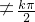 ,k∈Z}},则M的真子集个数为
,k∈Z}},则M的真子集个数为
- A.3
- B.7
- C.15
- D.无穷多个
B
分析:根据正切和余切的定义求出函数的定义域,分四种情况由三角函数值的符号,去掉绝对值求解集合M,即可得出它的真子集个数.
解答:由题意知,函数的定义域是{x|x≠ ,k∈Z},
,k∈Z},
下面由各个象限中三角函数值的符号来确定在各个象限中函数的值:
当x是第一象限角时,因所有三角函数值大于零,故y=4;
当x是第二象限角时,因为只有正弦值大于零,故y=1-1-1-1=-2;
当x是第三象限角时,因为正切值和余切值大于零,故y=-1-1+1+1=0;
当x是第四象限角时,因为只有余弦值大于零,故y=-2;
所以M={-2,0,4}.因为集合M中有3个元素,所以集合M子集有23=8个,
则集合M的非空子集的个数是8-1=7.
故选B.
点评:本题主要考查了子集与真子集,三角函数的定义以及符号,根据定义求出函数的定义域,由三角函数值的符号进行化简求值.
分析:根据正切和余切的定义求出函数的定义域,分四种情况由三角函数值的符号,去掉绝对值求解集合M,即可得出它的真子集个数.
解答:由题意知,函数的定义域是{x|x≠
 ,k∈Z},
,k∈Z},下面由各个象限中三角函数值的符号来确定在各个象限中函数的值:
当x是第一象限角时,因所有三角函数值大于零,故y=4;
当x是第二象限角时,因为只有正弦值大于零,故y=1-1-1-1=-2;
当x是第三象限角时,因为正切值和余切值大于零,故y=-1-1+1+1=0;
当x是第四象限角时,因为只有余弦值大于零,故y=-2;
所以M={-2,0,4}.因为集合M中有3个元素,所以集合M子集有23=8个,
则集合M的非空子集的个数是8-1=7.
故选B.
点评:本题主要考查了子集与真子集,三角函数的定义以及符号,根据定义求出函数的定义域,由三角函数值的符号进行化简求值.

练习册系列答案
相关题目
 },则M的真子集个数为( )
},则M的真子集个数为( ) ,x
,x ,k∈Z}},则M的真子集个数为( )
,k∈Z}},则M的真子集个数为( )