题目内容
（理科）△ABC中，已知∠A=
，边BC=2
，设∠B=x，△ABC的周长为y．
（1）求函数y=f（x）的解析式，并写出函数的定义域；
（2）求函数y=f（x）的值域．
| π |
| 3 |
| 3 |
（1）求函数y=f（x）的解析式，并写出函数的定义域；
（2）求函数y=f（x）的值域．
（1）△ABC的内角和A+B+C=π，且A=
，B=x，C＞0，
∴C=
-x＞0，0＜x＜
．
由正弦定理，知
=
=
，
即
所以y=4sinx+4sin(
-x)+2
(0＜x＜
)；
（2）由（1）知，
y=4sinx+4sin(
-x)+2
(0＜x＜
)
=6sinx+2
cosx+2
=4
sin(x+
)+2
(
＜x+
＜
)，
由正弦函数的图象知，当
＜x+
＜
时，有
＜sin(x+
)≤1．
于是，4
＜4
sin(x+
)+2
≤6
，
所以，函数y=4sinx+4sin(
-x)+2
(0＜x＜
)的值域是(4
，6
]．
| π |
| 3 |
∴C=
| 2π |
| 3 |
| 2π |
| 3 |
由正弦定理，知
2
| ||
sin
|
| b |
| sinx |
| c | ||
sin(
|
即
|
所以y=4sinx+4sin(
| 2π |
| 3 |
| 3 |
| 2π |
| 3 |
（2）由（1）知，
y=4sinx+4sin(
| 2π |
| 3 |
| 3 |
| 2π |
| 3 |
=6sinx+2
| 3 |
| 3 |
=4
| 3 |
| π |
| 6 |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
由正弦函数的图象知，当
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
于是，4
| 3 |
| 3 |
| π |
| 6 |
| 3 |
| 3 |
所以，函数y=4sinx+4sin(
| 2π |
| 3 |
| 3 |
| 2π |
| 3 |
| 3 |
| 3 |
练习册系列答案
浙江名校名师金卷系列答案
全优冲刺100分系列答案
相关题目
且
，
，则a＋c的最大值为
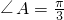，边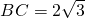
，设∠B=x，△ABC的周长为y．
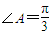，边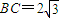
，设∠B=x，△ABC的周长为y．