题目内容
已知直线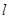 垂直于直线
垂直于直线 ,则直线
,则直线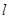 的斜率为( )
的斜率为( )
A. | B. | C.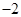 | D.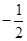 |
B
解析试题分析:因为直线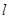 垂直于直线
垂直于直线 ,而利用直线
,而利用直线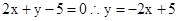 ,由斜截式方程可知,其斜率为-2,因此直线L的斜率为其负倒数,即为
,由斜截式方程可知,其斜率为-2,因此直线L的斜率为其负倒数,即为 ,那么可知选B.
,那么可知选B.
考点:本试题主要考查了两直线的垂直的位置关系的运用。
点评:解决该试题的关键是理解垂直时斜率是否存在,如果存在则斜率之积是否为1呢?注意要对于有参数的直线的垂直问题讨论k的存在与否。

练习册系列答案
相关题目
已知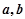 满足
满足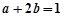 ,则直线
,则直线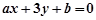 必过定点 ( )
必过定点 ( )
A.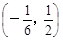 | B.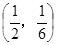 | C.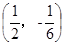 | D.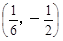 |
若两直线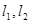 的倾斜角分别为
的倾斜角分别为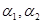 ,则下列四个命题中正确的是( )
,则下列四个命题中正确的是( )
A.若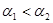 ,则两直线的斜率: ,则两直线的斜率: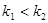 |
B.若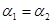 ,则两直线的斜率: ,则两直线的斜率: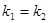 |
C.若两直线的斜率: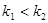 ,则 ,则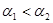 |
D.若两直线的斜率: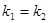 ,则 ,则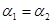 |
设直线 :
: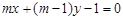 ,圆
,圆 :
: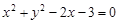 ,则( )
,则( )
A.对任意实数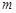 ,直线 ,直线 恒过定点 恒过定点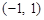 |
B.存在实数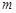 ,使直线 ,使直线 与圆 与圆 无公共点 无公共点 |
C.若圆 上存在两点关于直线 上存在两点关于直线 对称,则 对称,则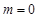 |
D.若直线 与圆 与圆 相交于 相交于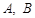 两点,则 两点,则 的最小值是 的最小值是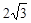 |
已知点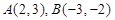 ,若直线
,若直线 过点
过点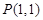 与线段
与线段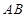 相交,则直线
相交,则直线 的斜率
的斜率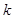 的取值范围是( )
的取值范围是( )
A.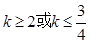 | B.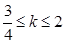 |
C.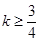 | D.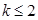 |
已知直线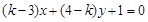 与
与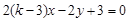 平行,则
平行,则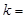 ( )
( )
| A.3 | B.3或5 | C.5 | D.2 |
过点A(1,2)且与原点距离最大的直线方程是( )
A.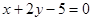 | B.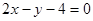 |
C.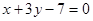 | D.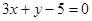 |
过点(1,0)且与直线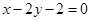 平行的直线方程是( )
平行的直线方程是( )
A.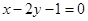 | B.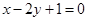 |
C. | D.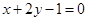 |
已知点P(3,2)与点Q(1,4)关于直线l对称,则直线l的方程为
A.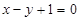 | B.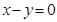 | C.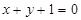 | D.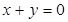 |