题目内容
(本题满分12分)
已知锐角△ABC中,角A、B、C的对边分别为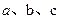 ,
,
且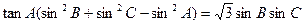 .
.
(1)求角A;
(2)求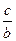 的范围.
的范围.
已知锐角△ABC中,角A、B、C的对边分别为
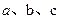 ,
,且
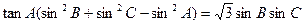 .
.(1)求角A;
(2)求
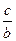 的范围.
的范围.(1)由tanA(sin2B+sin2C-sin2A)=sinBsinC得:
tanA(b2+c2-a2)=bc ① ………………2分
由余弦定理得:b2+c2-a2=2bc·cosA ② ………………4分
由①②得:sinA=,∴A= ………………6分
(2)∵△ABC是锐角三角形,又A=,∴<B<, tanB> ……………8分
∵ ====+ ……………10分
∴< <2 ……………12分
tanA(b2+c2-a2)=bc ① ………………2分
由余弦定理得:b2+c2-a2=2bc·cosA ② ………………4分
由①②得:sinA=,∴A= ………………6分
(2)∵△ABC是锐角三角形,又A=,∴<B<, tanB> ……………8分
∵ ====+ ……………10分
∴< <2 ……………12分
略

练习册系列答案
相关题目

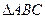 的3个顶点为
的3个顶点为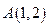 ,
,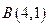 ,
,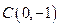 (1)求
(1)求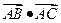 的值;
的值;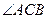 的大小,并判断
的大小,并判断 中,若
中,若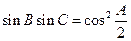 ,则此三角形为___
,则此三角形为___ ___.
___.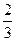 ,那么PC与平面
,那么PC与平面 ABC所成的角是( )
ABC所成的角是( )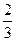
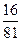
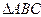 中,角
中,角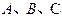 所对的边分别为
所对的边分别为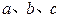 ,已知
,已知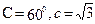 ,求使得ab取得最大值时的该三
,求使得ab取得最大值时的该三 角形面积为( )
角形面积为( ) 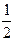
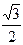


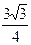
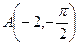 ,
,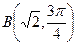 ,
,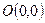 ,则
,则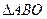 为( )
为( )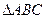 中,三个内角
中,三个内角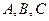 所对的边分别是
所对的边分别是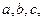 已知
已知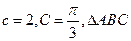 的面积等于
的面积等于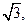
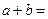 ____★____.
____★____.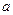 ,
,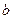 ,
,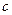 ,若∠C=120°,
,若∠C=120°,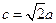 ,则
,则 ★ .
★ .