题目内容
已知集合A=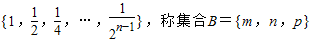
（其中m，n，p∈A）为集合A的一个三元子集，设A的所有三元子集的元素之和是Sn，则
= ．
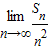【答案】分析：根据排列组合的知识可知集合A中的每一个元素被选到的可能有Cn-12种，从而求出A的所有三元子集的元素之和是Sn，最后利用极限的求解方法求出所求即可．
解答：解：集合A中有n个元素，从中选三个元素构成一个集合有Cn3个
集合A中的每一个元素被选到的可能有Cn-12种
∴A的所有三元子集的元素之和是Sn=Cn-12（1+
+
+…
）
=
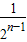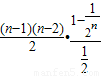=（n-1）（n-2）（1-
）
∴
=
[
-
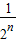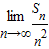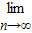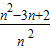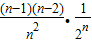]=1
故答案为：1
点评：本题主要考查了等比数列的求和，以及排列组合的有关知识，同时考查了极限的求解，有一定的难度．
解答：解：集合A中有n个元素，从中选三个元素构成一个集合有Cn3个
集合A中的每一个元素被选到的可能有Cn-12种
∴A的所有三元子集的元素之和是Sn=Cn-12（1+
++…）=
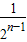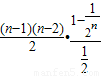=（n-1）（n-2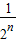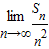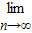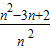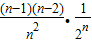）（1-）∴
=[-]=1故答案为：1
点评：本题主要考查了等比数列的求和，以及排列组合的有关知识，同时考查了极限的求解，有一定的难度．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目