题目内容
已知函数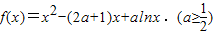
(1)若
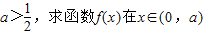 上的最大值;
上的最大值;(2)若对任意x∈(0,a)时,恒有ma-f(x)>1成立,求实数m的取值范围.
【答案】分析:(1)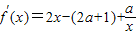 =
=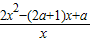 ,令f′(x)=0,得
,令f′(x)=0,得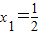 ,x2=a.由此进行分类讨论,能求出函数f(x)的最大值.
,x2=a.由此进行分类讨论,能求出函数f(x)的最大值.
(2)由(1)知:当a= 时,函数f(x)在(0,a),即(0,
时,函数f(x)在(0,a),即(0, )上单调递增;a
)上单调递增;a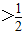 时,函数f(x)在(0,a)上的最大值为f(
时,函数f(x)在(0,a)上的最大值为f( ).故“恒有ma-f(x)>1成立”等价于“ma-1>f(
).故“恒有ma-f(x)>1成立”等价于“ma-1>f( )恒成立”,由此能求出实数m的取值范围.
)恒成立”,由此能求出实数m的取值范围.
解答:解:(1)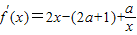 =
=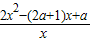 ,
,
令f′(x)=0,得 ,x2=a.
,x2=a.
∵a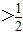 ,∴由f′(x)>0,得函数f(x)在(0,
,∴由f′(x)>0,得函数f(x)在(0, )上单调递增,
)上单调递增,
由f′(x)<0得函数f(x)在( )上单调递减.
)上单调递减.
∴函数f(x)的最大值为f( )=
)=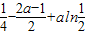 =aln
=aln -a-
-a- .
.
(2)由(1)知:
当①a= 时,函数f(x)在(0,a),即(0,
时,函数f(x)在(0,a),即(0, )上单调递增;
)上单调递增;
②a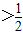 时,函数f(x)在(0,a)上的最大值为f(
时,函数f(x)在(0,a)上的最大值为f( ).
).
∴“恒有ma-f(x)>1成立”等价于“ma-1>f( )恒成立”,
)恒成立”,
即ma-1>f( )=aln
)=aln -a-
-a- ,
,
∴m>ln -1+
-1+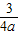 .
.
∵a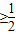 ,∴ln
,∴ln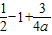 的最大值为
的最大值为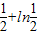 ,
,
∴实数m的取值范围为{m|m>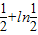 }.
}.
点评:本题考查函数最大值的求法,考查满足条件的实数的取值范围的求法,考查推理论证能力、运算推导能力、等价转化能力、分类讨论能力.解题时要认真审题,仔细解答,注意导数性质的灵活运用.
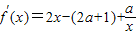 =
=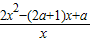 ,令f′(x)=0,得
,令f′(x)=0,得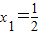 ,x2=a.由此进行分类讨论,能求出函数f(x)的最大值.
,x2=a.由此进行分类讨论,能求出函数f(x)的最大值.(2)由(1)知:当a=
 时,函数f(x)在(0,a),即(0,
时,函数f(x)在(0,a),即(0, )上单调递增;a
)上单调递增;a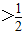 时,函数f(x)在(0,a)上的最大值为f(
时,函数f(x)在(0,a)上的最大值为f( ).故“恒有ma-f(x)>1成立”等价于“ma-1>f(
).故“恒有ma-f(x)>1成立”等价于“ma-1>f( )恒成立”,由此能求出实数m的取值范围.
)恒成立”,由此能求出实数m的取值范围.解答:解:(1)
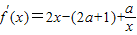 =
=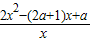 ,
,令f′(x)=0,得
 ,x2=a.
,x2=a.∵a
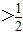 ,∴由f′(x)>0,得函数f(x)在(0,
,∴由f′(x)>0,得函数f(x)在(0, )上单调递增,
)上单调递增,由f′(x)<0得函数f(x)在(
 )上单调递减.
)上单调递减.∴函数f(x)的最大值为f(
 )=
)=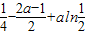 =aln
=aln -a-
-a- .
.(2)由(1)知:
当①a=
 时,函数f(x)在(0,a),即(0,
时,函数f(x)在(0,a),即(0, )上单调递增;
)上单调递增;②a
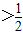 时,函数f(x)在(0,a)上的最大值为f(
时,函数f(x)在(0,a)上的最大值为f( ).
).∴“恒有ma-f(x)>1成立”等价于“ma-1>f(
 )恒成立”,
)恒成立”,即ma-1>f(
 )=aln
)=aln -a-
-a- ,
,∴m>ln
 -1+
-1+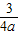 .
.∵a
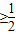 ,∴ln
,∴ln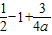 的最大值为
的最大值为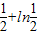 ,
,∴实数m的取值范围为{m|m>
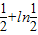 }.
}.点评:本题考查函数最大值的求法,考查满足条件的实数的取值范围的求法,考查推理论证能力、运算推导能力、等价转化能力、分类讨论能力.解题时要认真审题,仔细解答,注意导数性质的灵活运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 的图象上横坐标为
的图象上横坐标为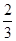 的点处存在垂直于y 轴的切线,求a 的值;
的点处存在垂直于y 轴的切线,求a 的值; 的图象与函数
的图象与函数