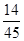题目内容
已知盒中有10个灯泡,其中8个正品,2个次品.需要从中取出2个正品,每次取出1个,取出后不放回,直到取出2个正品为止.设ξ为取出的次数,求ξ的分布列及Eξ.
解:由题意知每次取1件产品,
∴至少需2次,即ξ最小为2,有2件次品,
当前2次取得的都是次品时,ξ=4,
∴ξ可以取2,3,4
当变量是2时,表示第一次取出正品,第二次取出也是正品,
根据相互独立事件同时发生的概率公式得到
P(ξ=2)= ×
× =
= ;
;
P(ξ=3)= ×
× ×
× +
+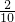 ×
× ×
× =
= ;
;
P(ξ=4)=1- -
- =
= .
.
∴ξ的分布列如下:

Eξ=2×P(ξ=2)+3×P(ξ=3)+4×P(ξ=4)= .
.
分析:由题意知每次取1件产品,至少需2次,即ξ最小为2,有2件次品,当前2次取得的都是次品时ξ=4,得到变量的取值,当变量是2时,表示第一次取出正品,第二次取出也是正品,根据相互独立事件同时发生的概率公式得到分布列,写出期望.
点评:本题考查离散型随机变量的分布列和数学期望的概念,考查运用概率知识解决实际问题的能力.遇到求用至少来表述的事件的概率时,往往先求它的对立事件的概率.
∴至少需2次,即ξ最小为2,有2件次品,
当前2次取得的都是次品时,ξ=4,
∴ξ可以取2,3,4
当变量是2时,表示第一次取出正品,第二次取出也是正品,
根据相互独立事件同时发生的概率公式得到
P(ξ=2)=
 ×
× =
= ;
;P(ξ=3)=
 ×
× ×
× +
+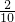 ×
× ×
× =
= ;
;P(ξ=4)=1-
 -
- =
= .
.∴ξ的分布列如下:

Eξ=2×P(ξ=2)+3×P(ξ=3)+4×P(ξ=4)=
 .
.分析:由题意知每次取1件产品,至少需2次,即ξ最小为2,有2件次品,当前2次取得的都是次品时ξ=4,得到变量的取值,当变量是2时,表示第一次取出正品,第二次取出也是正品,根据相互独立事件同时发生的概率公式得到分布列,写出期望.
点评:本题考查离散型随机变量的分布列和数学期望的概念,考查运用概率知识解决实际问题的能力.遇到求用至少来表述的事件的概率时,往往先求它的对立事件的概率.

练习册系列答案
相关题目
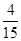 B.
B.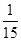 C.
C.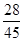 D.
D.