题目内容
若实数a∈（1，2），则使得函数f(x)=
x2-ax+(a-1)lnx单调递减的一个区间是（ ）
| 1 |
| 2 |
| A、（1，+∞） |
| B、（0，a-1） |
| C、（0，1） |
| D、（a-1，1） |
分析：先求出函数的导数，令导数小于0，求出单调区间，再比对四个选项得出正确答案．
解答：解：f′(x)=x-a+
=
由函数的解析式知，x＞0，令f'（x）＜0得[x-（a-1）]（x-1）＜0
又∵a∈（1，2），∴a-1∈（0，1）
∴a-1＜x＜1
故选D
| a-1 |
| x |
| [x-(a-1)](x-1) |
| x |
由函数的解析式知，x＞0，令f'（x）＜0得[x-（a-1）]（x-1）＜0
又∵a∈（1，2），∴a-1∈（0，1）
∴a-1＜x＜1
故选D
点评：本题考查利用层数研究函数的单调性，求解本题关键是正确得出函数的导函数，以及根据函数的定义域将所得的不等式转化如x＞0，令f'（x）＜0得[x-（a-1）]（x-1）＜0，
练习册系列答案
相关题目
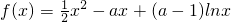单调递减的一个区间是