题目内容
长度都为2的向量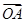 ,
,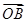 的夹角为
的夹角为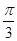 ,点C在以O为圆心的圆弧AB(劣弧)上,
,点C在以O为圆心的圆弧AB(劣弧)上,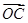 =m
=m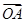 +n
+n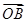 ,则m+n的最大值是________.
,则m+n的最大值是________.
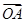 ,
,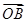 的夹角为
的夹角为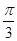 ,点C在以O为圆心的圆弧AB(劣弧)上,
,点C在以O为圆心的圆弧AB(劣弧)上,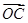 =m
=m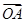 +n
+n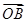 ,则m+n的最大值是________.
,则m+n的最大值是________.
建立平面直角坐标系,设向量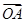 =(2,0),向量
=(2,0),向量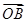 =(1,
=(1,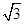 ).设向量
).设向量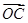 =(2cos α,2sin α),0≤α≤
=(2cos α,2sin α),0≤α≤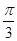 .由
.由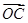 =m
=m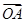 +n
+n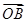 ,得(2cos α,2sin α)=(2m+n,
,得(2cos α,2sin α)=(2m+n,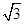 n),
n),
即2cos α=2m+n,2sin α=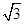 n,
n,
解得m=cos α- sin α,n=
sin α,n= sin α.
sin α.
故m+n=cos α+ sin α=
sin α= sin
sin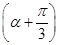 ≤
≤ .
.
 =(2,0),向量
=(2,0),向量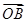 =(1,
=(1,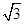 ).设向量
).设向量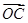 =(2cos α,2sin α),0≤α≤
=(2cos α,2sin α),0≤α≤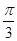 .由
.由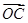 =m
=m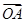 +n
+n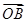 ,得(2cos α,2sin α)=(2m+n,
,得(2cos α,2sin α)=(2m+n,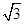 n),
n),即2cos α=2m+n,2sin α=
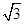 n,
n,解得m=cos α-
 sin α,n=
sin α,n= sin α.
sin α.故m+n=cos α+
 sin α=
sin α= sin
sin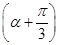 ≤
≤ .
.
练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
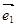 ,
,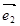 ,
,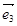 ,
,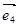 是某平面内的四个单位向量,其中
是某平面内的四个单位向量,其中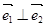 ,
,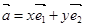 ,规定经过一次“斜二测变换”得到向量
,规定经过一次“斜二测变换”得到向量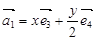 ,设向量
,设向量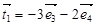 是向量
是向量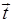 经过一次“斜二测变换”得到的向量,则
经过一次“斜二测变换”得到的向量,则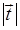 是( )
是( )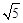
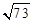
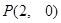 ,正方形
,正方形 内接于⊙
内接于⊙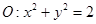 ,
, 、
、 分别为边
分别为边 、
、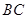 的中点,当正方形
的中点,当正方形 旋转时,
旋转时,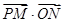 的取值范围是( )
的取值范围是( )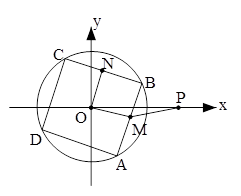
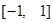
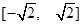
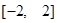
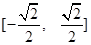
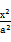 -
-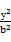 =1(a>0,b>0)上的点,F1,F2是其焦点,双曲线的离心率是
=1(a>0,b>0)上的点,F1,F2是其焦点,双曲线的离心率是 ,且
,且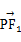 ·
·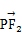 =0,若△PF1F2的面积为9,则a+b的值为( )
=0,若△PF1F2的面积为9,则a+b的值为( ) 中,
中,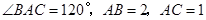 ,
,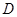 是
是 边上一点,
边上一点,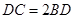 ,则
,则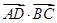 等于( )
等于( )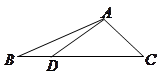
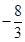
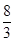
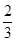
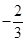
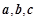 满足
满足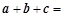 0,向量
0,向量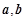 的夹角为
的夹角为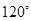 ,且
,且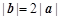 ,则向量
,则向量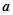 与
与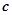 的夹角为 .
的夹角为 .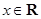 ,向量
,向量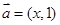 ,
,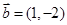 ,且
,且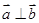 ,则
,则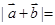 .
.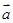 ,
,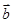 满足
满足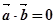 ,
,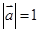 ,
,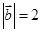 ,则
,则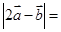 _________.
_________.