题目内容
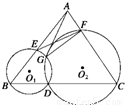
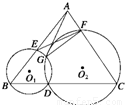
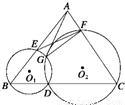
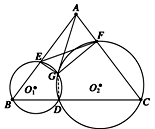
如图所示,已知D为△ABC的BC边
上一点,⊙O1经过点B,D,交AB于另一点E,⊙O2经过
点C,D,交AC于另一点F,⊙O1与⊙O2交于点G.
(1)求证:∠EAG=∠EFG;
(2)若⊙O2的半径为5,圆心O2到直线AC的距离为3,AC=10,AG切⊙O2于G,求线段AG的长.
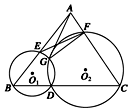
(1)证明略(2)AG=2![]() .
.
解析:
(1)证明 连接GD,因为四边形BDGE,CDGF分别内接于⊙O1,⊙O2,∴∠AEG=∠BDG,∠AFG=∠CDG,
又∠BDG+∠CDG=180°,∴∠AEG+∠AFG=180°.
即A,E,G,F四点共圆,∴∠EAG=∠EFG.
(2)解 因为⊙O2的半径为5,圆心O2到直线AC的距离为3,所以由垂径定理知FC=2![]() =8,又AC=10,∴AF=2,∵AG切⊙O2于G,∴AG2=AF·AC=2×10=20,AG=2
=8,又AC=10,∴AF=2,∵AG切⊙O2于G,∴AG2=AF·AC=2×10=20,AG=2![]() .
.

练习册系列答案
相关题目
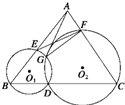 如图所示,已知D为△ABC的BC边上一点,⊙O1经过点B,D,交AB于另一点E,⊙O2经过点C,D,交
如图所示,已知D为△ABC的BC边上一点,⊙O1经过点B,D,交AB于另一点E,⊙O2经过点C,D,交