题目内容
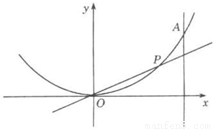
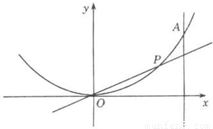
设点P在曲线y=x2+2上,点Q在曲线 上,则|PQ|的最小值等于 .
上,则|PQ|的最小值等于 .
【答案】分析:曲线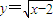 的图象在第一象限,要使曲线y=x2+2上的点与曲线
的图象在第一象限,要使曲线y=x2+2上的点与曲线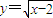 上的点取得最小值,点P应在曲线y=x2+2的第一象限内的图象上,分析可知y=x2+2(x≥0)与
上的点取得最小值,点P应在曲线y=x2+2的第一象限内的图象上,分析可知y=x2+2(x≥0)与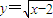 互为反函数,它们的图象关于直线y=x对称,所以,求出
互为反函数,它们的图象关于直线y=x对称,所以,求出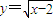 上点Q到直线y=x的最小值,乘以2即可得到|PQ|的最小值.
上点Q到直线y=x的最小值,乘以2即可得到|PQ|的最小值.
解答:解:由y=x2+2,得:x2=y-2,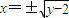 .
.
所以,y=x2+2(x≥0)与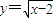 互为反函数.
互为反函数.
它们的图象关于y=x对称.
P在曲线y=x2+2上,点Q在曲线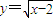 上,
上,
设P(x,x2),Q(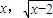 )
)
要使|PQ|的距离最小,则P应在y=x2+2(x≥0)上,
又P,Q的距离为P或Q中一个点到y=x的最短距离的两倍.
以Q点为例,Q点到直线y=x的最短距离
d= =
=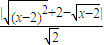 =
=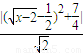 .
.
所以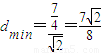 .
.
则|PQ|的最小值等于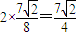 .
.
故答案为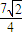 .
.
点评:本题考查了反函数,考查了互为反函数图象之间的关系,考查了数学转化思想,解答此题的关键是把求两曲线上点的最小距离问题,转化为求一支曲线上的动点到定直线的最小距离问题,此题是中档题.
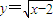 的图象在第一象限,要使曲线y=x2+2上的点与曲线
的图象在第一象限,要使曲线y=x2+2上的点与曲线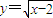 上的点取得最小值,点P应在曲线y=x2+2的第一象限内的图象上,分析可知y=x2+2(x≥0)与
上的点取得最小值,点P应在曲线y=x2+2的第一象限内的图象上,分析可知y=x2+2(x≥0)与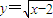 互为反函数,它们的图象关于直线y=x对称,所以,求出
互为反函数,它们的图象关于直线y=x对称,所以,求出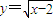 上点Q到直线y=x的最小值,乘以2即可得到|PQ|的最小值.
上点Q到直线y=x的最小值,乘以2即可得到|PQ|的最小值.解答:解:由y=x2+2,得:x2=y-2,
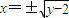 .
.所以,y=x2+2(x≥0)与
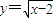 互为反函数.
互为反函数.它们的图象关于y=x对称.
P在曲线y=x2+2上,点Q在曲线
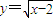 上,
上,设P(x,x2),Q(
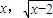 )
)要使|PQ|的距离最小,则P应在y=x2+2(x≥0)上,
又P,Q的距离为P或Q中一个点到y=x的最短距离的两倍.
以Q点为例,Q点到直线y=x的最短距离
d=
 =
=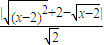 =
=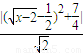 .
.所以
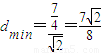 .
.则|PQ|的最小值等于
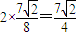 .
.故答案为
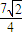 .
.点评:本题考查了反函数,考查了互为反函数图象之间的关系,考查了数学转化思想,解答此题的关键是把求两曲线上点的最小距离问题,转化为求一支曲线上的动点到定直线的最小距离问题,此题是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
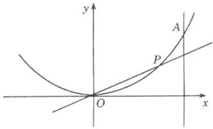 设点P在曲线y=x2上,从原点向A(2,4)移动,如果直线OP,曲线y=x2及直线x=2所围成的面积分别记为S1、S2.
设点P在曲线y=x2上,从原点向A(2,4)移动,如果直线OP,曲线y=x2及直线x=2所围成的面积分别记为S1、S2.