Question

直线：y=

3

3

x+

3

与圆心为D的圆：(x-

3

)2+(y-1)2=3交于A、B两点，则直线AD与BD的倾斜角之和为（　　）

• A．

  7

  6

  π
• B．

  5

  4

  π
• C．

  4

  3

  π
• D．

  5

  3

  π

Answer 1

分析：根据题目条件画出圆的图象与直线的图象，再利用圆的性质建立两个倾斜角的等量关系，化简整理即可求出．

解答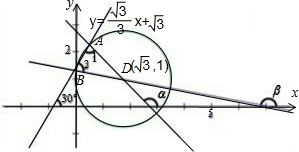：解：令直线AD与BD的倾斜角α、β
直线y=

3

3

x+

3

的斜率为

3

3

，所以它的倾斜角为：

π

6

，
画出直线与圆的图象，
由图象及三角形的外角与不相邻的内角关系，
可知：∠1=α-

π

6

，∠2=

π

6

+π-β．
由圆的性质可知，直线AD，BD过圆心，三角形ABD是等腰三角形，
∴∠1=∠2，
∴α-

π

6

=

π

6

+π-β，
故α+β=

4π

3

，
故选C．

点评：本题主要考查了圆的方程与直线方程的位置关系，直线的倾斜角，三角形的角的关系，直线和圆的方程的应用，属于中档题．