题目内容
已知圆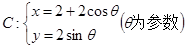
，直线l:
（1）求圆C的普通方程.若以原点为极点，以x轴的正半轴为极轴建立极坐标系，写出圆C的极坐标方程.
（2）判断直线l与圆C的位置关系，并说明理由；若相交，请求出弦长
【答案】
（1）
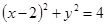---------2分
---------------5分
（2）解法一：由于直线l过圆心
，-------6分所以直线与圆相交-----8分
弦长为4---------10分
解法二：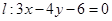
-----------6分
圆心到直线的距离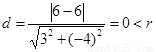
，所以直线与圆相交-------------8分
由于直线l过圆心，所以弦长为4
【解析】I）利用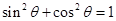
,消去参数即可.利用极坐标方程与普通方程相互转化公式
即可求得圆的极坐标方程.
(II)要把圆和直线都化成普通方程，然后利用圆心到直线的距离与半径进行比较判断直线与圆的位置关系，d>r
相交;d=r 相切； d<r 相离.再利用
求弦长即可.
练习册系列答案
相关题目
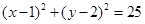,直线L: 
取什么实数，L与圆恒交于两点；
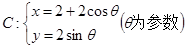，直线l: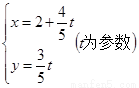
及直线l：x-y+3=O，当直线l被圆C截得的
时，则a=（ ）
（B）
（C）
（D）
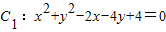与直线l：x+2y-4=0相交于A，B两点．