题目内容
以点A(4,-3)为直角顶点的Rt△OAB中,|AB|=2|OA|且点B纵坐标大于0.(1)求向量
. | AB |
(2)求圆x2-6x+y2+2y=0关于直线OB对称的圆的方程.
分析:(1)设出
=(μ,u),利用垂直和|AB|=2|OA|,B纵坐标大于0,求得μ,u.
(2)先求圆心和半径,再求对称圆心坐标,可得对称圆的方程.
. |
| AB |
(2)先求圆心和半径,再求对称圆心坐标,可得对称圆的方程.
解答:解:(1)设
=(μ,u),则由
得
或
由
=
+
=(μ+4,u-3),且u-3>0
∴u=8
=(6,8).
(2)圆x2-6x+y2+2y=0的标准方程是(x-3)2+(y+1)2=10
∴圆心为(3,-1),半径为
由(1)知B(10,5),直线OB的方程为y=
x
设(3,-1)关于OB的对称点为(x,y)则
∴
∴所求圆方程为(x-1)2+(y-3)2=10.
. |
| AB |
|
|
|
由
. |
| OB |
. |
| OA |
. |
| AB |
∴u=8
. |
| AB |
(2)圆x2-6x+y2+2y=0的标准方程是(x-3)2+(y+1)2=10
∴圆心为(3,-1),半径为
| 10 |
由(1)知B(10,5),直线OB的方程为y=
| 1 |
| 2 |
设(3,-1)关于OB的对称点为(x,y)则
|
∴
|
∴所求圆方程为(x-1)2+(y-3)2=10.
点评:本题考查平面向量的数量积,垂直的条件,点关于直线对称的点的坐标的求法,是中档题,近年高考热点.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
 的坐标;
的坐标;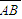 的坐标;
的坐标;