题目内容
若不等式x>0,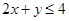 与
与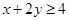 所确定的平面区域被直线
所确定的平面区域被直线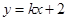 分为面积相等的两部分,则k的值是( )
分为面积相等的两部分,则k的值是( )
| A.1 | B. 2 | C.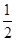 | D.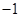 |
A
解析考点:二元一次不等式(组)与平面区域.
分析:先画出不等式组 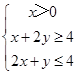 所表示的平面区域,求出平面区域的面积以及在直线y="kx+2" 一侧的面积;再结合平面区域被直线y="kx+2" 分为面积相等的两部分即可求出k的值.
所表示的平面区域,求出平面区域的面积以及在直线y="kx+2" 一侧的面积;再结合平面区域被直线y="kx+2" 分为面积相等的两部分即可求出k的值.
解:不等式组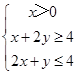 所表示的平面区域为三角形ABC.
所表示的平面区域为三角形ABC.
由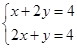 ?
? .故点C(
.故点C(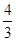 ,
,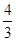 ).
).
由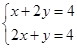 ?
?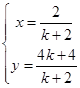 ,故点D(
,故点D(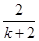 ,
,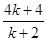 )
)
所以 S△ABD=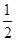 ×|AB|?xD=
×|AB|?xD=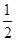 x2×
x2×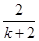 =
=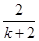 .
.
S△ABC=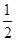 ×|AB|?xC=
×|AB|?xC=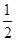 ×2×
×2×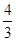 =
=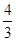 .
.
又因为平面区域被直线y="kx+2" 分为面积相等的两部分
∴S△ABD=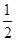 S△ABC即
S△ABC即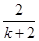 =
=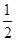 ×
×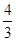 ,解得k=1.
,解得k=1.
故选A.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
探究函数![]() ,x∈(0,+∞)的最小值,并确定相应的x的值,列表如下:
,x∈(0,+∞)的最小值,并确定相应的x的值,列表如下:
| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.102 | 4.24 | 4.3 | 5 | 5.8 | 7.57 | … |
请观察表中y值随x值变化的特点,完成下列问题:
(1)若函数![]() ,(x>0)在区间(0,2)上递减,则在 上递增;
,(x>0)在区间(0,2)上递减,则在 上递增;
(2)当x= 时,![]() ,(x>0)的最小值为 ;
,(x>0)的最小值为 ;
(3)试用定义证明![]() ,(x>0)在区间(0,2)上递减;
,(x>0)在区间(0,2)上递减;
(4)函数![]() ,(x<0)有最值吗?是最大值还是最小值?此时x为何值?
,(x<0)有最值吗?是最大值还是最小值?此时x为何值?
(5)解不等式![]() .
.
解题说明:(1)(2)两题的结果直接填写在横线上;(4)题直接回答,不需证明。
 的一个焦点为(
的一个焦点为( ,0),一条渐近线方程为
,0),一条渐近线方程为 ,其中
,其中
 .
. 的通项公式;
的通项公式;  ;
; +
+ (a>0,且a≠1)对一切自然数n恒成立,求实数x的取值范围.
(a>0,且a≠1)对一切自然数n恒成立,求实数x的取值范围.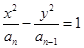 的一个焦点为(
的一个焦点为(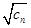 ,0),一条渐近线方程为
,0),一条渐近线方程为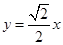 ,其中
,其中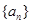
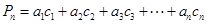 .
.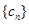 的通项公式;
的通项公式; 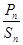 ;
;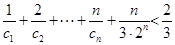 +
+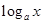 (a>0,且a≠1)对一切自然数n恒成立,求实数x的取值范围.
(a>0,且a≠1)对一切自然数n恒成立,求实数x的取值范围.