题目内容
(本题满分10分)已知集合A=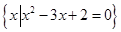 ,B=
,B=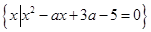 .若A∩B=B,求实数
.若A∩B=B,求实数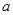 的取值范围.
的取值范围.
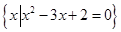 ,B=
,B=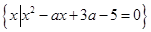 .若A∩B=B,求实数
.若A∩B=B,求实数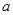 的取值范围.
的取值范围.当2≤a<10时,均有A∩B=B.
本试题主要是考查了函数与参数的一元二次方程的解集问题的运用,以及结合的交集的运算。先分析集合A,然后因为A∩B=B,则说明 ,那么可知需要对于参数a分情况讨论得到结论。
,那么可知需要对于参数a分情况讨论得到结论。
解: A={x|x2-3x+2=0}={1,2},由x2-ax+3a-5=0,知Δ=a2-4(3a-5)=a2-12a+20=(a-2)(a-10).
(1)当2<a<10时,Δ<0,B=
 A;
A;
(2)当a≤2或a≥10时,Δ≥0,则B≠ .若x=1,则1-a+3a-5=0,得a=2,此时B={x|x2-2x+1=0}={1}
.若x=1,则1-a+3a-5=0,得a=2,此时B={x|x2-2x+1=0}={1} A;
A;
若x=2,则4-2a+3a-5=0,得a=1,此时B={2,-1} A.
A.
综上所述,当2≤a<10时,均有A∩B=B.
 ,那么可知需要对于参数a分情况讨论得到结论。
,那么可知需要对于参数a分情况讨论得到结论。解: A={x|x2-3x+2=0}={1,2},由x2-ax+3a-5=0,知Δ=a2-4(3a-5)=a2-12a+20=(a-2)(a-10).
(1)当2<a<10时,Δ<0,B=

 A;
A;(2)当a≤2或a≥10时,Δ≥0,则B≠
 .若x=1,则1-a+3a-5=0,得a=2,此时B={x|x2-2x+1=0}={1}
.若x=1,则1-a+3a-5=0,得a=2,此时B={x|x2-2x+1=0}={1} A;
A;若x=2,则4-2a+3a-5=0,得a=1,此时B={2,-1}
 A.
A. 综上所述,当2≤a<10时,均有A∩B=B.

练习册系列答案
相关题目
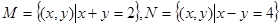 ,那么集合
,那么集合 。
。 , A=
, A= 2,4
2,4 , B="{3,4}," 则A∪B = ( )
, B="{3,4}," 则A∪B = ( )
 ,若
,若 .
. 的取值范围.
的取值范围.  B,求实数a的取值集合.
B,求实数a的取值集合.
 ,
, ,则
,则  ( )
( ) 



 ,
, ,且
,且 ,那么
,那么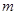 的值可以是( )
的值可以是( ) 

 ,
, ,则
,则 (
(
 )
) ______.
______. ,
,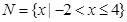 ,则
,则



