题目内容
甲、乙两艘轮船驶向一个不能同时停泊两艘轮船的码头,它们在一昼夜内任何时刻到达是等可能的.(1)如果甲船和乙船的停泊时间都是4小时,求它们中的任何一条船 不需要等等码头空出的概率;
(2)如果甲船的停泊时间为4小时,乙船的停泊时间是2小时,求它们中的任何一条船 不需要等待码头空出的概率.
【答案】分析:(1)如果甲船和乙船的停泊时间都是4小时,设甲、乙两船到达时间分别为x、y,我们可以画出(x,y)点对称的平面区域,及满足条件y-x>4或y-x<-4平面区域,分别求出对应面积,代入几何概型公式,即可求出答案.
(2)如果甲船的停泊时间为4小时,乙船的停泊时间是2小时,求出满足条件y-x>4或y-x>2对应的平面区域的面积,代入几何概型公式,即可求出答案.
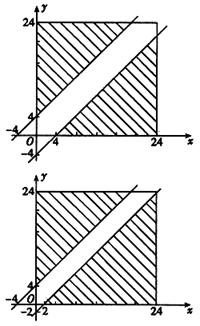
解答:解:(1)设甲、乙两船到达时间分别为x、y,则O≤x<24,0≤y<24且y-x>4或y-x<-4
作出区域
设“两船无需等待码头空出”为事件A,则
P(A)=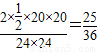 .
.
(2)当甲船的停泊时间为4小时,两船不需等待码头空出,则满足x-y>2.设在上述条件时“两船不需等待码头空出”为事件B,画出区域.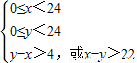 ,
,
P(B)= .
.
点评:本题考查 的知识点是几何概型,其中求出所有基本事件对应的平面区域的面积,及满足条件 的平面区域的面积是解答本题的关键.
(2)如果甲船的停泊时间为4小时,乙船的停泊时间是2小时,求出满足条件y-x>4或y-x>2对应的平面区域的面积,代入几何概型公式,即可求出答案.
解答:解:(1)设甲、乙两船到达时间分别为x、y,则O≤x<24,0≤y<24且y-x>4或y-x<-4
作出区域

设“两船无需等待码头空出”为事件A,则
P(A)=
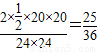 .
.(2)当甲船的停泊时间为4小时,两船不需等待码头空出,则满足x-y>2.设在上述条件时“两船不需等待码头空出”为事件B,画出区域.
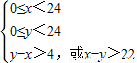 ,
,P(B)=
 .
.点评:本题考查 的知识点是几何概型,其中求出所有基本事件对应的平面区域的面积,及满足条件 的平面区域的面积是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目