题目内容
已知向量 =(cos
=(cos x,sin
x,sin x),
x), 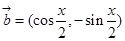 ,且x∈[0,
,且x∈[0, ].
].
(1)求
(2)设函数 =
= +
+ ,求函数
,求函数 的最值及相应的
的最值及相应的 的值。
的值。
【答案】
(1)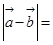
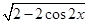 =2sinx
=2sinx
(2) 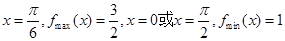
【解析】
试题分析:(1)由已知条件: 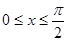 , 得:
, 得:


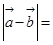
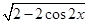 =2sinx
=2sinx
(2) 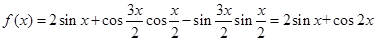
=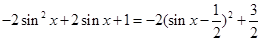

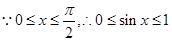
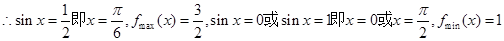
考点:本题主要考查平面向量的坐标运算,三角函数的和差倍半公式,三角函数的图象和性质,二次函数的性质。
点评:典型题,本题首先从平面向量的坐标运算入手,得到三角函数式,为研究三角函数的图象和性质,由利用三角函数和差倍半公式等,将函数“化一”,这是常考题型。首先运用“三角公式”进行化简,为进一步解题奠定了基础。涉及向量模的计算,依然要注意“化模为方”,本题较为容易。

练习册系列答案
相关题目
 =(cos
=(cos x,sin
x,sin =(
=( ),函数
),函数 ,
,
 ,则下列性质正确的是
,则下列性质正确的是
 的最小正周期为
的最小正周期为 B.函数
B.函数 为奇函数
为奇函数 递减
D.函数
递减
D.函数