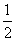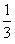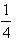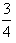Question

若?b∈（0，1），则方程x²+x+b=0有实根的概率为（　　）

• A、

  1

  2

• B、

  1

  3

• C、

  1

  4

• D、

  3

  4

Answer 1

分析：由题意知本题是一个几何概型，试验包含的所有事件是?b∈（0，1），而满足条件的事件是使得方程x²+x+b=0有实根的b的值，根据一元二次方程根与系数的关系得到满足条件的b的值，得到结果．

解答：解：由题意知本题是一个几何概型，
试验包含的所有事件是?b∈（0，1），
而满足条件的事件是使得方程x²+x+b=0有实根的b的值，
要使方程x²+x+b=0有实根，
△=1-4b≥0
∴b≤

1

4

，
∴在基本事件包含的范围之内b∈(0，

1

4

)，
由几何概型公式得到P=

1

4

，
故选C．

点评：古典概型和几何概型是我们学习的两大概型，古典概型要求能够列举出所有事件和发生事件的个数，而不能列举的就是几何概型，几何概型的概率的值是通过长度、面积、和体积、的比值得到．