题目内容
设抛物线M:y2=2px(p>0)的焦点F是双曲线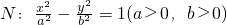 右焦点.若M与N的公共弦AB恰好过F,则双曲线N的离心率e的值为
右焦点.若M与N的公共弦AB恰好过F,则双曲线N的离心率e的值为
- A.

- B.

- C.
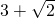
- D.2
B
分析:先根据抛物线方程得到焦点坐标和交点坐标,代入双曲线,结合 =c通过联立,得到关于离心率e的方程,进而可求得e.
=c通过联立,得到关于离心率e的方程,进而可求得e.
解答:由题意,交点为( ,p),代入双曲线方程得
,p),代入双曲线方程得
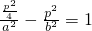 ,又
,又 =c
=c
∴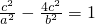 ,化简得 c4-6a2c2+a4=0
,化简得 c4-6a2c2+a4=0
∴e4-6e2+1=0
e2=3+2 =(1+
=(1+ )2,
)2,
∴e= +1
+1
故选B.
点评:本题主要考查了抛物线的应用.要求学生对圆锥曲线的知识能综合掌握.考查计算能力,本题解题的关键是判断出两曲线的交点坐标为( ,±p).
,±p).
分析:先根据抛物线方程得到焦点坐标和交点坐标,代入双曲线,结合
 =c通过联立,得到关于离心率e的方程,进而可求得e.
=c通过联立,得到关于离心率e的方程,进而可求得e.解答:由题意,交点为(
 ,p),代入双曲线方程得
,p),代入双曲线方程得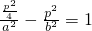 ,又
,又 =c
=c∴
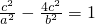 ,化简得 c4-6a2c2+a4=0
,化简得 c4-6a2c2+a4=0∴e4-6e2+1=0
e2=3+2
 =(1+
=(1+ )2,
)2,∴e=
 +1
+1故选B.
点评:本题主要考查了抛物线的应用.要求学生对圆锥曲线的知识能综合掌握.考查计算能力,本题解题的关键是判断出两曲线的交点坐标为(
 ,±p).
,±p). 
练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
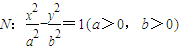 右焦点.若M与N的公共弦AB恰好过F,则双曲线N的离心率e的值为( )
右焦点.若M与N的公共弦AB恰好过F,则双曲线N的离心率e的值为( )
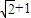
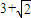
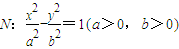 右焦点.若M与N的公共弦AB恰好过F,则双曲线N的离心率e的值为( )
右焦点.若M与N的公共弦AB恰好过F,则双曲线N的离心率e的值为( )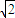
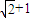
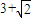
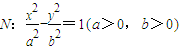 右焦点.若M与N的公共弦AB恰好过F,则双曲线N的离心率e的值为( )
右焦点.若M与N的公共弦AB恰好过F,则双曲线N的离心率e的值为( )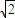
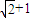
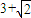
 右焦点.若M与N的公共弦AB恰好过F,则双曲线N的离心率e的值为( )
右焦点.若M与N的公共弦AB恰好过F,则双曲线N的离心率e的值为( )

