题目内容
设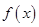 定义在R且x不为零的偶函数,在区间
定义在R且x不为零的偶函数,在区间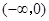 上递增, f(xy)=f(x)+f(y),当a满足
上递增, f(xy)=f(x)+f(y),当a满足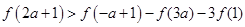 则a的取值范围是( )。
则a的取值范围是( )。
A.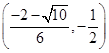 |
B.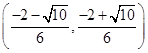 |
C.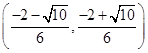 且a 且a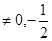 |
D.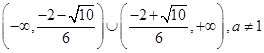 |
C
解析解:由f(xy)=f(x)+f(y)?f(1×1)=f(1)+f(1)?f(1)=0;
∴f(2a+1)>f(-a+1)-f(3a)-3f(1)
?f(2a+1)+f(3a)>f(-a+1)
?f[(2a+1)3a]>f(-a+1);①
∵f(x)定义在R且x不为零的偶函数;
∴①转化为f(|3a(2a+1)|)>f(|-a+1|)②
∵函数在区间(-∞,0)上递增,
∴函数在区间(0,+∞)上递增,
∴②转化为|3a(2a+1)|<|-a+1|?[3a(2a+1)]2<(-a+1)2?[3a(2a+1)-(-a+1)][3a(2a+1)+(-a+1)]<0?(6a2+2a+1)(6a2+4a-1)<0;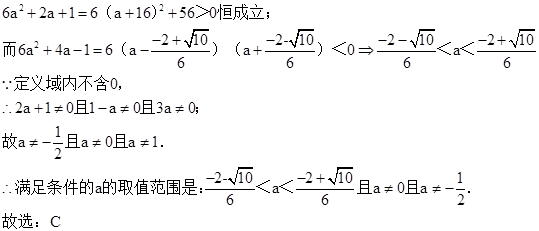

 名校课堂系列答案
名校课堂系列答案“a>0”是“方程 至少有一个负数根”的 ( ▲ )
至少有一个负数根”的 ( ▲ )
| A.充分必要条件 | B.必要不充分条件 |
| C.充分不必要条件 | D.既不充分也不必要条件 |
设 ,则
,则 的大小关系是
的大小关系是
A. | B. | C. | D. |
若函数 满足
满足 的解集是( )
的解集是( )
A. | B. | C. | D. |
某企业去年销售收入1000万元,年成本为生产成本500万元与年广告成本200万元两部分.若年利润必须按p%纳税,且年广告费超出年销售收入2%的部分也按p%纳税,其他不纳税.已知该企业去年共纳税120万元.则税率p%为( )
| A.10% | B.12% | C.25% | D.40% |
设函数
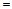
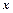 |
|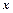 | + b
| + b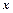 + c 给出下列四个命题:
+ c 给出下列四个命题:
①c = 0时,y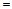
 是奇函数 ②b
是奇函数 ②b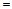 0 , c >0时,方程
0 , c >0时,方程
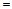 0 只有一个实根
0 只有一个实根
③y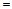
 的图象关于(0 , c)对称 ④方程
的图象关于(0 , c)对称 ④方程
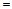 0至多两个实根
0至多两个实根
其中正确的命题是 ( )
| A.①、④ | B.①、③ | C.①、②、③ | D.①、②、④ |
若函数y=loga|x-2|(a>0且a≠1)在区间(1,2)上是增函数,则f(x)在区间(2,
+∞)上的单调性为 ( )
| A.先增后减 | B.先减后增 |
| C.单调递增 | D.单调递减 |
当 时,不等式
时,不等式 恒成立,则实数
恒成立,则实数 的取值范围为 ( )
的取值范围为 ( )
A. | B. | C. | D. |
 ,对任意的x∈[0,1]恒有f(x+a)≤f(x)成立,则实数a的取值范围是 .
,对任意的x∈[0,1]恒有f(x+a)≤f(x)成立,则实数a的取值范围是 .