题目内容
某西部山区的某种特产由于运输的原因,长期只能在当地销售,当地政府对该项特产的销售投资收益为:每投入x万元,可获得利润P=![]() (x-40)2+100万元.当地政府拟在新的十年发展规划中加快发展此特产的销售,其规划方案为:在规划前后对该项目每年都投入60万元的销售投资,在未来10年的前5年中,每年都从60万元中拨出30万元用于修建一条公路,5年修成,通车前该特产只能在当地销售;公路通车后的5年中,该特产既在本地销售,也在外地销售,在外地销售的投资收益为:每投入x万元,可获利润Q=
(x-40)2+100万元.当地政府拟在新的十年发展规划中加快发展此特产的销售,其规划方案为:在规划前后对该项目每年都投入60万元的销售投资,在未来10年的前5年中,每年都从60万元中拨出30万元用于修建一条公路,5年修成,通车前该特产只能在当地销售;公路通车后的5年中,该特产既在本地销售,也在外地销售,在外地销售的投资收益为:每投入x万元,可获利润Q=![]() (60-x)2+
(60-x)2+![]() (60-x)万元.问从10年的累积利润看,该规划方案是否可行?
(60-x)万元.问从10年的累积利润看,该规划方案是否可行?
答案:
解析:
解析:
|
解:在实施规划前,由题设P= 则10年的总利润为W1=100×10=1000(万元). 实施规划后的前5年中,由题设P= 前5年的利润和为 设在公路通车的后5年中,每年用x万元投资于本地的销售,而用剩下的(60-x)万元用于外地区的销售投资,则其总利润为 W2=[ 当x=30时,[W2]max=4950(万元). 从而10年的总利润为 故该规划方案有极大实施价值. |

练习册系列答案
相关题目
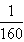 (x-40)2+100万元(已扣除投资,下同)。当地政府拟在新的十年发展规划中加快发展此特产的销售,其规划方案为:在未来10年内对该项目每年都投入60万元的销售资金,其中在前5年中,每年都从60万元中拨出30万元用于修建一条公路。公路5年建成,通车前该特产只能在当地销售;公路通车后的5年中,该特产既在本地销售,也在外地销售.在外地销售的投资收益为:每投入x万元,可获纯利润Q=
(x-40)2+100万元(已扣除投资,下同)。当地政府拟在新的十年发展规划中加快发展此特产的销售,其规划方案为:在未来10年内对该项目每年都投入60万元的销售资金,其中在前5年中,每年都从60万元中拨出30万元用于修建一条公路。公路5年建成,通车前该特产只能在当地销售;公路通车后的5年中,该特产既在本地销售,也在外地销售.在外地销售的投资收益为:每投入x万元,可获纯利润Q=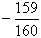 (60-x)2+
(60-x)2+ (60-x)万元,问仅从这10年的累积利润看,该规划方案是否可行?
(60-x)万元,问仅从这10年的累积利润看,该规划方案是否可行?