题目内容
如果无穷数列{an}满足下列条件:①
≤an+1;②存在实数M,使an≤M.其中n∈N*,那么我们称数列{an}为Ω数列.
(1)设数列{bn}的通项为bn=5n-2n,且是Ω数列,求M的取值范围;
(2)设{cn}是各项为正数的等比数列,Sn是其前项和,c3=
,S3=
证明:数列{Sn}是Ω数列;
(3)设数列{dn}是各项均为正整数的Ω数列,求证:dn≤dn+1.
| an+an+2 |
| 2 |
(1)设数列{bn}的通项为bn=5n-2n,且是Ω数列,求M的取值范围;
(2)设{cn}是各项为正数的等比数列,Sn是其前项和,c3=
| 1 |
| 4 |
| 7 |
| 4 |
(3)设数列{dn}是各项均为正整数的Ω数列,求证:dn≤dn+1.
(1)∵bn+1-bn=5-2n,∴n≥3,bn+1-bn<0,故数列{bn}单调递减;(3分)
当n=1,2时,bn+1-bn>0,即b1<b2<b3,
则数列{bn}中的最大项是b3=7,所以M≥7.(4分)
(2)证明:∵{cn}是各项正数的等比数列,Sn是其前n项和,c3=
,S3=
设其公比为q>0,∴
+
+c3=
.(6分)
整理,得6q2-q-1=0,解得q=
,q=-
(舍去).
∴c1=1,cn=
,Sn=2-
=Sn+2,S<2.(8分)
对任意的n∈N*,有
=2-
-
<2-
=Sn+1,且Sn<2,
故{Sn}是Ω数列.(10分)
(3)证明:假设存在正整数k使得dk>dk+1成立,由数列{dn}的各项均为正整数,可得dk≥dk+1+1,即dk+1≤dk-1.
因为
≤dk+1,所以dk+2≤2dk+1-dk≤2(dk-1)-dk=dk-2.
由dk+2≤2dk+1-dk及dk>dk+1得dk+2<2dk+1-dk+1=dk+1,故dk+2≤dk+1-1.
因为
≤dk+2,所以dk+3≤2dk+2-dk+1≤2(dk+1-1)-dk+1=dk+1-2≤dk-3,
由此类推,可得dk+m≤dk-m(m∈N*).(14分)
又存在M,使dk≤M,∴m>M,使dk+m<0,这与数列{dn}的各项均为正数矛盾,所以假设不成立,
即对任意n∈N*,都有dk≤dk+1成立.(16分)
当n=1,2时,bn+1-bn>0,即b1<b2<b3,
则数列{bn}中的最大项是b3=7,所以M≥7.(4分)
(2)证明:∵{cn}是各项正数的等比数列,Sn是其前n项和,c3=
| 1 |
| 4 |
| 7 |
| 4 |
设其公比为q>0,∴
| c3 |
| q2 |
| c3 |
| q |
| 7 |
| 4 |
整理,得6q2-q-1=0,解得q=
| 1 |
| 2 |
| 1 |
| 3 |
∴c1=1,cn=
| 1 |
| 2n-1 |
| 1 |
| 2n |
对任意的n∈N*,有
| Sn+Sn+2 |
| 2 |
| 1 |
| 2n |
| 1 |
| 2n+2 |
| 1 |
| 2n+1 |
故{Sn}是Ω数列.(10分)
(3)证明:假设存在正整数k使得dk>dk+1成立,由数列{dn}的各项均为正整数,可得dk≥dk+1+1,即dk+1≤dk-1.
因为
| dk+dk+2 |
| 2 |
由dk+2≤2dk+1-dk及dk>dk+1得dk+2<2dk+1-dk+1=dk+1,故dk+2≤dk+1-1.
因为
| dk+1+dk+3 |
| 2 |
由此类推,可得dk+m≤dk-m(m∈N*).(14分)
又存在M,使dk≤M,∴m>M,使dk+m<0,这与数列{dn}的各项均为正数矛盾,所以假设不成立,
即对任意n∈N*,都有dk≤dk+1成立.(16分)

练习册系列答案
相关题目
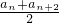 ≤an+1;②存在实数M,使an≤M.其中n∈N*,那么我们称数列{an}为Ω数列.
≤an+1;②存在实数M,使an≤M.其中n∈N*,那么我们称数列{an}为Ω数列. ,S3=
,S3= 证明:数列{Sn}是Ω数列;
证明:数列{Sn}是Ω数列;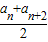 ≤an+1;②存在实数M,使an≤M.其中n∈N*,那么我们称数列{an}为Ω数列.
≤an+1;②存在实数M,使an≤M.其中n∈N*,那么我们称数列{an}为Ω数列. ,S3=
,S3= 证明:数列{Sn}是Ω数列;
证明:数列{Sn}是Ω数列;