题目内容
在△ABC中,求分别满足下列条件的三角形形状:①B=60°,b2=ac;②b2tanA=a2tanB;
③sinC=
| sinA+sinB | cosA+cosB |
分析:①根据余弦定理可求出a=c,再由B=60°可判断三角形是等边三角形.
②根据正弦定理将边的关系转化为角的正弦的关系,再由二倍角公式可得到A与B的关系,进而得到答案.
③根据正弦定理将角的正弦关系转化为边的关系,再由余弦定理可得三边满足勾股数,进而可判断三角形的形状.
④利用两角和公式对等式进行化简整理,求得
=
,利用正弦定理转化成角的正弦,进而约分求得sin2A=sin2B,进而确定A,B的关系,确定三角形的形状
②根据正弦定理将边的关系转化为角的正弦的关系,再由二倍角公式可得到A与B的关系,进而得到答案.
③根据正弦定理将角的正弦关系转化为边的关系,再由余弦定理可得三边满足勾股数,进而可判断三角形的形状.
④利用两角和公式对等式进行化简整理,求得
| sinAcosB |
| cosAsinB |
| a2 |
| b2 |
解答:解:①由余弦定理cos60°=
?
=
?a2+c2-ac=ac
∴(a-c)2=0,∴a=c.由a=c及B=60°可知△ABC为等边三角形.
②由b2tanA=a2tanB?
=
?
=
=
∴sinAcosA=sinBcosB,∴sin2A=sin2B,∴A=B或A+B=90°,
∴△ABC为等腰△或Rt△.
③∵sinC=
,由正弦定理:c(cosA+cosB)=a+b,
再由余弦定理:c×
+c×
=a+b
∴(a+b)(c2-a2-b2)=0,∴c2=a2+b2,∴△ABC为Rt△.
④∵(a2-b2)sin(A+B)=(a2+b2)sin(A-B).
∴(a2-b2)(sinAcosB+cosAsinB)=(a2+b2)(sinAcosB-cosAsinB).
整理求得a2cosAsinB=b2sinAcosB,
即:
=
=
∴sin2A=sin2B,
∴A=B或A+B=
∵
=
=2R,
∴△ABC是等腰△或Rt△.
| a2+c2-b2 |
| 2ac |
| a2+c2-b2 |
| 2ac |
| 1 |
| 2 |
∴(a-c)2=0,∴a=c.由a=c及B=60°可知△ABC为等边三角形.
②由b2tanA=a2tanB?
| b2sinA |
| cosA |
| a2sinB |
| cosB |
| sinBcosA |
| sinAcosB |
| b2 |
| a2 |
| sin2B |
| sin2A |
∴△ABC为等腰△或Rt△.
③∵sinC=
| sinA+sinB |
| cosA+cosB |
再由余弦定理:c×
| a2+b2-c2 |
| 2bc |
| a2+c2-b2 |
| 2ac |
∴(a+b)(c2-a2-b2)=0,∴c2=a2+b2,∴△ABC为Rt△.
④∵(a2-b2)sin(A+B)=(a2+b2)sin(A-B).
∴(a2-b2)(sinAcosB+cosAsinB)=(a2+b2)(sinAcosB-cosAsinB).
整理求得a2cosAsinB=b2sinAcosB,
即:
| sinAcosB |
| cosAsinB |
| a2 |
| b2 |
| sin2A |
| sin2B |
∴sin2A=sin2B,
∴A=B或A+B=
| π |
| 2 |
∵
| a |
| sinA |
| b |
| sinB |
∴△ABC是等腰△或Rt△.
点评:这类判定三角形形状的问题的一般解法是:由正弦定理或余弦定理将已知条件转化为只含边的式子或只含角的三角函数式,然后化简考查边或角的关系,从而确定三角形的形状.有时一个条件既可用正弦定理也可用余弦定理甚至可以混用.如本例的②④也可用余弦定理,请同学们试试看.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
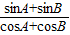 .
.