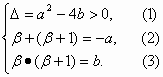Question

设g(x)＝x³＋ax²＋bx图象上任一点P(x，y)处切线的斜率为f(x)，且方程f(x)＝0的两根为α、β(a、b∈R)．

(1)若α＝β＋1，且β∈Z，求证：f(－a)＝(a²－1)；

(2)若α、β∈(2，3)，试证明存在整数k，使得|f(k)|≤．

Answer 1

答案：
解析：

解析：(1)证明：由题意，知f(x)＝(x)＝x2＋ax＋b， 　　则 　　由②，得β＝－(a＋1)，代入③整理，得a2－4b＝1，且满足①，则b＝(a2－1)．从而 　　f(－a)＝(－a)2＋a(－a)＋b＝b＝(a2－1)． 　　(2)证明：因为α、β∈(2，3)，而f(x)＝x2＋ax＋b＝(x－α)(x－β)， 　　∴|f(2)|·|f(3)| 　　＝|(2－α)(2－β)||(3－α)(3－β)| 　　＝|(α－2)(3－α)|·|(β－2)(3－β)|≤＝()2，即|f(2)||f(3)|≤()2， 　　必有|f(2)|≤或|f(3)|≤， 　　∴存在整数k＝2或k＝3使|f(k)|≤．