题目内容
求圆心为(2,1),且与已知圆x2+y2-3x=0的公共弦所在直线过点(5,-2)的圆的方程.
圆的方程为(x-2)2+(y-1)2=4.
设所求圆的方程为(x-2)2+(y-1)2=r2,
即x2+y2-4x-2y+5-r2=0.①
已知圆的方程为x2+y2-3x=0,②
②-①,得公共弦所在直线方程为x+2y-5+r2=0.
又此直线过点(5,-2),
∴5-4-5+r2=0.∴r2=4.
故所求圆的方程为(x-2)2+(y-1)2=4.
即x2+y2-4x-2y+5-r2=0.①
已知圆的方程为x2+y2-3x=0,②
②-①,得公共弦所在直线方程为x+2y-5+r2=0.
又此直线过点(5,-2),
∴5-4-5+r2=0.∴r2=4.
故所求圆的方程为(x-2)2+(y-1)2=4.

练习册系列答案
相关题目
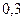 ),求
),求 的正切值;
的正切值;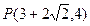 作一条直线和
作一条直线和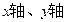 分别相交于
分别相交于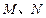 两点,试求
两点,试求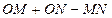 的最大值。(其中
的最大值。(其中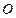 为坐标原点)
为坐标原点) 的动圆与y轴交于M、N两点,C(-1,0),D(1,0)是x轴上两点,直线MC与
的动圆与y轴交于M、N两点,C(-1,0),D(1,0)是x轴上两点,直线MC与 ND相交于P。
ND相交于P。 (O是坐标原点),求点O到直线GH的距离。
(O是坐标原点),求点O到直线GH的距离。
 (–2≤x≤2)与直线y=r(x–2)+4有两个交点时,实数r的取值范围 .
(–2≤x≤2)与直线y=r(x–2)+4有两个交点时,实数r的取值范围 .