题目内容
7．设平面向量组$\overrightarrow{a}$i（i=1，2，3，…）满足：①|$\overrightarrow{a}$i|=1；②$\overrightarrow{a}$i•$\overrightarrow{a}$i+1=0，则|$\overrightarrow{a}$1+$\overrightarrow{a}$2|=$\sqrt{2}$，|$\overrightarrow{a}$1+$\overrightarrow{a}$2+$\overrightarrow{a}$3|的最大值为$\sqrt{5}$．分析 由已知条件便知$\overrightarrow{{a}_{i}}$为单位向量，并且相邻的向量互相垂直，这样可用有向线段来表示$\overrightarrow{{a}_{i}}$，根据图形即可得出答案．
解答 解：根据条件知：向量组$\overrightarrow{{a}_{i}}$里的每个向量都是单位向量，且相邻的向量垂直；
∴向量$\overrightarrow{{a}_{1}}+\overrightarrow{{a}_{2}}$用有向线段表示如下：
∴$|\overrightarrow{{a}_{1}}+\overrightarrow{{a}_{2}}|=\sqrt{2}$；
当$|\overrightarrow{{a}_{1}}+\overrightarrow{{a}_{2}}+\overrightarrow{{a}_{3}}|$取最大值时，用有向线段表示如下：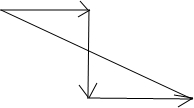
∴$|\overrightarrow{{a}_{1}}+\overrightarrow{{a}_{2}}+\overrightarrow{{a}_{3}}|$的最大值为$\sqrt{5}$．
故答案为：$\sqrt{2}，\sqrt{5}$．
点评 考查向量长度的概念，向量垂直的充要条件，用有向线段表示向量，以及用有向线段解决向量问题的方法．
练习册系列答案
相关题目
．
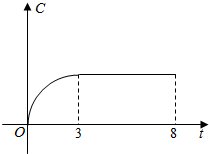某工厂近8年来产品总量C与时间t（年）的关系如图所示，则下列说法中正确的序号是②③．