题目内容
在等腰△
中，
是腰
的中点，若
，则
( )
A． | B． | C． | D． |
A
解析试题分析：因为若，所以
，如图所示，
设
，则
，
设
，由余弦定理可得，
，
，
将上面的值代入两式相加可得，
，
再由余弦定理可得，
，
即
考点：将，可解得
，在三角形
中，利用余弦定理可得
，从而得
考点：解三角形．
练习册系列答案
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
第三学期赢在暑假系列答案
相关题目
设
的内角
所对边的长分别为
,若
,则角
=( )
A． | B． | C． | D． |
设
的内角
所对的边长分别为
，且
，
,则
的最小值是（ ）
| A．2 | B．3 | C．4 | D．5 |
设锐角
的三内角
、
、
所对边的边长分别为
、
、
，且
，
,则
的取值范围为（ ）.
A． | B． | C． ． | D． |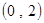
在
中，已知
分别为内角
，
，
所对的边，
为的面积.若向量
满足
，则
（ ）
A． | B． | C． | D． |
在
中，角
所对边的长分别为
，若
，则
的最小值为（ ）
A． | B． | C． | D． |
在△ABC中，若
，
，此三角形面积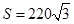
，则a的值是( )
A． | B．75 | C．51 | D．49 |
中，角
所对的边分别为
，若
，则
（ ）
A． | B． | C． | D． |