题目内容
(选做题)已知直线的极坐标方程为ρsin(θ+
)=
,圆M的参数方程为
(θ为参数).
(Ⅰ)求圆M上的点到直线的距离的最小值;
(Ⅱ)若过点C(2,0)的直线l与圆M交于A、B两点,且
=
,求直线l的斜率.
| π |
| 4 |
| ||
| 2 |
|
(Ⅰ)求圆M上的点到直线的距离的最小值;
(Ⅱ)若过点C(2,0)的直线l与圆M交于A、B两点,且
| CA |
| AB |
分析:(1)把圆的参数方程化为普通方程,把直线的极坐标方程化为直角坐标方程,求出圆心到直线的距离,把此距离再减去半径,即得所求.
(2)设出直线l的参数方程,代入圆M的方程化简,根据参数的几何意义以及韦达定理,求得cosθ+sinθ=
,再利用同角三角函数的基本关系求出tanθ的值,即为所求.
(2)设出直线l的参数方程,代入圆M的方程化简,根据参数的几何意义以及韦达定理,求得cosθ+sinθ=
3
| ||
| 4 |
解答:解:(1)圆M的普通方程为x2+(y+2)2=4,圆心M(0,-2),半径等于2.直线的极坐标方程ρsin(θ+
)=
,即x+y-1=0.
圆心到直线x+y-1=0的距离d=
,
∴圆M上的点到直线的距离的最小值为
-2.
(2)设直线l的参数方程是
(t为参数),代入圆M的方程得:t2+(4cosθ+4sinθ)t+4=0,
由t的几何意义及
=
知,t1=2t2且t1+t2=-4cosθ-4sinθ,t1t2=4.
结合几何图形知,t<0,∴t1=2t2=-2
,
∴-4cosθ-4sinθ=-3
,即cosθ+sinθ=
.
∴sinθcosθ=
,∴tanθ=4±
,
∴直线l的斜率是4±
.
| π |
| 4 |
| ||
| 2 |
圆心到直线x+y-1=0的距离d=
3
| ||
| 2 |
∴圆M上的点到直线的距离的最小值为
3
| ||
| 2 |
(2)设直线l的参数方程是
|
由t的几何意义及
| CA |
| AB |
结合几何图形知,t<0,∴t1=2t2=-2
| 2 |
∴-4cosθ-4sinθ=-3
| 2 |
3
| ||
| 4 |
∴sinθcosθ=
| 1 |
| 16 |
| 15 |
∴直线l的斜率是4±
| 15 |
点评:本题主要考查把参数方程化为普通方程的方法,参数的几何意义,把极坐标方程化为直角坐标方程的方法,点到直线的距离公式的应用,直线和圆的位置关系的应用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的参数方程为:
的参数方程为: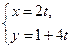 (
(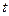 为参数),圆
为参数),圆 的极坐标方程为
的极坐标方程为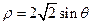 ,则直线
,则直线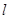 的参数方程为:
的参数方程为: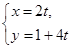 (
(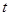 为参数),圆
为参数),圆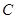 的极坐标方程为
的极坐标方程为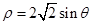 ,则直线
,则直线