题目内容
若A={2,4,a3-2a2-a+7},B={1,a+1,a2-2a+2,-
(a2-3a-8),a3+a2+3a+7},且A∩B={2,5},试求实数a.
| 1 | 2 |
分析:利用A∩B={2,5},说明2,5∈A,则必有a3-2a2-a+7=5,然后求解a,进行检验.
解答:解:因为A∩B={2,5},所以2,5∈A,则必有a3-2a2-a+7=5,解得a=2或a=±1.
当a=1时,a2-2a+2=1,与元素的互异性矛盾,所以a=1不成立.
当a=-1时,集合a={2,4,5},B={1,0,2,4,5},此时A∩B={2,4,5},与A∩B={2,5}矛盾,所以a=-1不成立.
当a=2时,集合A={2,4,5},B={1,3,2,5,25},满足A∩B={2,5},所以a=2成立.
综上,满足条件的实数a=2.
当a=1时,a2-2a+2=1,与元素的互异性矛盾,所以a=1不成立.
当a=-1时,集合a={2,4,5},B={1,0,2,4,5},此时A∩B={2,4,5},与A∩B={2,5}矛盾,所以a=-1不成立.
当a=2时,集合A={2,4,5},B={1,3,2,5,25},满足A∩B={2,5},所以a=2成立.
综上,满足条件的实数a=2.
点评:本题主要考查了利用集合关系求参数取值问题,本题的难度在于如何求解三次方程,求出a之后要注意进行代入检验,防止出错.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
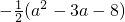 ,a3+a2+3a+7},且A∩B={2,5},试求实数a.
,a3+a2+3a+7},且A∩B={2,5},试求实数a. ,a3+a2+3a+7},且A∩B={2,5},试求实数a.
,a3+a2+3a+7},且A∩B={2,5},试求实数a.