题目内容
已知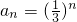 ,把数列{an}的各项排列成如下的三角形状:
,把数列{an}的各项排列成如下的三角形状:

记A(m,n)表示第m行的第n个数,则A(11,12)=
- A.
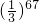
- B.
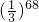
- C.
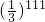
- D.
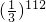
D
分析:①A(11,12)为三角形状的第11行的第12个数,根据题意得第11行的最后一个数是 =a121,
=a121,
②且有2×11-1=21个项,得到第11行得第一项为101+12-1=112,所以为a112求出即可.
解答:由A(m,n)表示第m行的第n个数可知,A(11,12)表示第11行的第12个数,
根据图形可知:①每一行的最后一个项的项数为行数的平方,所以第11行的最后一个项的项数为112=121,即为a121;
②每一行都有2n-1个项,所以第11行有2×11-1=21个项,得到第11行第一个项为121-21+1=101,所以第12项的项数为101+12-1=112;
所以A(11,12)=a112=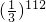 .
.
故选D
点评:考查学生利用数列的递推式解决数学问题的能力,会根据图形归纳总计得到一组数的规律.
分析:①A(11,12)为三角形状的第11行的第12个数,根据题意得第11行的最后一个数是
 =a121,
=a121,②且有2×11-1=21个项,得到第11行得第一项为101+12-1=112,所以为a112求出即可.
解答:由A(m,n)表示第m行的第n个数可知,A(11,12)表示第11行的第12个数,
根据图形可知:①每一行的最后一个项的项数为行数的平方,所以第11行的最后一个项的项数为112=121,即为a121;
②每一行都有2n-1个项,所以第11行有2×11-1=21个项,得到第11行第一个项为121-21+1=101,所以第12项的项数为101+12-1=112;
所以A(11,12)=a112=
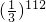 .
.故选D
点评:考查学生利用数列的递推式解决数学问题的能力,会根据图形归纳总计得到一组数的规律.

练习册系列答案
相关题目

 已知
已知 ,把数列{an}的各项排列成如图的三角形状,记A(m,n)表示第m行的第n个数,则A(10,12)=( )
,把数列{an}的各项排列成如图的三角形状,记A(m,n)表示第m行的第n个数,则A(10,12)=( )



 已知
已知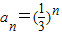 ,把数列{an}的各项排列成如图的三角形状,记A(m,n)表示第m行的第n个数,则A(10,12)=( )
,把数列{an}的各项排列成如图的三角形状,记A(m,n)表示第m行的第n个数,则A(10,12)=( )



 已知
已知 ,把数列{an}的各项排列成如图的三角形状,记A(m,n)表示第m行的第n个数,则A(10,12)=( )
,把数列{an}的各项排列成如图的三角形状,记A(m,n)表示第m行的第n个数,则A(10,12)=( )



 ,把数列{an}的各项排成如右图所示三角形形状,记A(m,n)表示第m行、第n列的项,则A(10,8)= ,a120在图中的位置为 .
,把数列{an}的各项排成如右图所示三角形形状,记A(m,n)表示第m行、第n列的项,则A(10,8)= ,a120在图中的位置为 .