题目内容
6.已知等比数列{an}满足2a1+a3=3a2,且a3+2是a2,a4的等差中项.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若${b_n}={a_n}+{log_{\frac{1}{2}}}{a_n}$,Sn=b1+b2+…+bn,求使Sn-2n+1+47<0成立的正整数n的最小值.
分析 (I)利用等比数列与等差数列的通项公式即可得出;
(II)bn=an+log2$\frac{1}{an}$=2n+log2$\frac{1}{2n}$=2n-n.利用等比数列与等差数列的前n项和公式即可得出Sn.再利用一元二次不等式的解法即可得出.
解答 解:(Ⅰ)设等比数列{an}的首项为a1,公比为q,
∵2a1+a3=3a2,且a3+2是a2,a4的等差中项
∴a1(2+q2)=3a1q ①,a1(q+q3)=2a1q2+4 ②
由①及a1≠0,得q2-3q+2=0,∴q=1,或q=2,
当q=1时,②式不成立;
当q=2时,符合题意,
把q=2代入②得a1=2,
∴an=2•2n-1=2n.
(Ⅱ)bn=an+log2$\frac{1}{an}$=2n+log2$\frac{1}{2n}$=2n-n.
∴Sn=2-1+22-2+23-3+…+2n-n
=(2+22+23+…+2n)-(1+2+3+…+n)
=$\frac{2(1-2n)}{1-2}$-$\frac{n(1+n)}{2}$=2n+1-2-$\frac{1}{2}$n-$\frac{1}{2}$n2.
∵Sn-2n+1+47<0,
∴2n+1-2-$\frac{1}{2}$n-$\frac{1}{2}$n2-2n+1+47<0,
即n2+n-90>0,解得n>9或n<-10.
∵n∈N*,故使Sn-2n+1+47<0成立的正整数n的最小值为10.
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式、一元二次不等式的解法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
14.设f(x)是奇函数,且在(0,+∞)内是减函数,又f(-3)=0,则(x2-2x-3)•f(x)≥0的解集是( )
| A. | {x|-1≤x≤3或x≤-3} | B. | {x|-1≤x≤0或x≤-3或x=3} | ||
| C. | {x|-3≤x≤-1或x≥3} | D. | {x|-1≤x≤0或x≥3或x=-3} |
1.函数y=1+sinx的部分图象如图所示,则该函数在[0,2π]的单调递减区间是( )
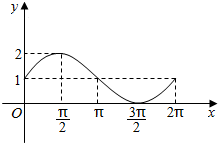

| A. | [0,π] | B. | [$\frac{π}{2}$,$\frac{3π}{2}$] | C. | [0,$\frac{3π}{2}$] | D. | [$\frac{π}{2}$,2π] |
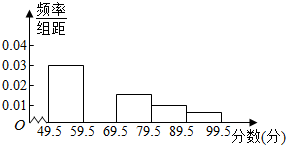 宜宾三中举行的电脑知识竞赛中,将高二年级两个班参赛的学生成绩(得分均为整数)进行整理后分成五组,绘制如图所示的频率分布直方图.已知图中从左到右的第一、三、四、五小组的频率分别是0.30,0.15,0.10,0.05.则第二小组的小长方形的高为( )
宜宾三中举行的电脑知识竞赛中,将高二年级两个班参赛的学生成绩(得分均为整数)进行整理后分成五组,绘制如图所示的频率分布直方图.已知图中从左到右的第一、三、四、五小组的频率分别是0.30,0.15,0.10,0.05.则第二小组的小长方形的高为( )