题目内容
(1)求曲线y = 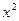 与直线y =" 3" x围成的图形的面积 ;
与直线y =" 3" x围成的图形的面积 ;
(2)若曲线y =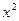 与直线y =" 3" x交于(a ,
与直线y =" 3" x交于(a ,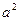 )(a>0)点 ,记曲线y =
)(a>0)点 ,记曲线y = 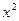 与直线y =" 3" x围成的图形的面积为S(a) ,判断S(a)的单调区间 ,求S(a)的极值 .
与直线y =" 3" x围成的图形的面积为S(a) ,判断S(a)的单调区间 ,求S(a)的极值 .
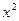 与直线y =" 3" x围成的图形的面积 ;
与直线y =" 3" x围成的图形的面积 ;(2)若曲线y =
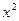 与直线y =" 3" x交于(a ,
与直线y =" 3" x交于(a ,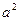 )(a>0)点 ,记曲线y =
)(a>0)点 ,记曲线y = 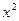 与直线y =" 3" x围成的图形的面积为S(a) ,判断S(a)的单调区间 ,求S(a)的极值 .
与直线y =" 3" x围成的图形的面积为S(a) ,判断S(a)的单调区间 ,求S(a)的极值 .(1)4

(2)当a = 3时S(a)有极大值 ,且极大值为S(3) = 4
 .
.解 :(1 ) 由 y = 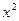 ,得两曲线的交点为(0,0),(3 ,0),由定积分的几何意义知 ,所求图形的面积为
,得两曲线的交点为(0,0),(3 ,0),由定积分的几何意义知 ,所求图形的面积为
S = =" 3" ·
=" 3" · -
- =
=  -
- =
=  = 4
= 4 ;
;
(2)由题意和定积分的几何意义知
S(a) = =
=  -
- ,
,
∴ =" 3" a-
=" 3" a-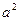 = -a(a-3),
= -a(a-3),
∴ 当a∈(0 ,3)时 ,S(a) 单调递增 ,当a∈(3 ,+∞)时 ,S(a) 单调递减 ,当a = 3时S(a)有极大值 ,且极大值为S(3) = 4 .
.
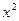 ,得两曲线的交点为(0,0),(3 ,0),由定积分的几何意义知 ,所求图形的面积为
,得两曲线的交点为(0,0),(3 ,0),由定积分的几何意义知 ,所求图形的面积为S =
 =" 3" ·
=" 3" · -
- =
=  -
- =
=  = 4
= 4 ;
;(2)由题意和定积分的几何意义知
S(a) =
 =
=  -
- ,
,∴
 =" 3" a-
=" 3" a-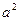 = -a(a-3),
= -a(a-3),∴ 当a∈(0 ,3)时 ,S(a) 单调递增 ,当a∈(3 ,+∞)时 ,S(a) 单调递减 ,当a = 3时S(a)有极大值 ,且极大值为S(3) = 4
 .
.
练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 ,则
,则 表示( )
表示( ) 为半径的球的体积的一半
为半径的球的体积的一半 ,坐标轴及
,坐标轴及 所围成的图形的面积
所围成的图形的面积
 的值为()
的值为()


 =
= ,则实数a等于( )
,则实数a等于( )

 的值是**********
的值是********** 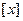 表示不超过
表示不超过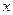 的最大整数,如
的最大整数,如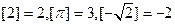 ,定义函数
,定义函数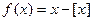 ,设函数
,设函数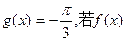 在区间
在区间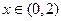 上零点的个数记为
上零点的个数记为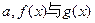 图象交点的个数记为
图象交点的个数记为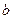 ,则
,则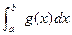 的值是 。
的值是 。 ,若
,若 ,则
,则 .
. 所围成的图形的面积 ( )
所围成的图形的面积 ( ) B
B  C
C  D
D 
 ,曲线
,曲线 及
及 轴所围图形的面积为 )
轴所围图形的面积为 )
