题目内容
(2x+4)2010=a0+a1x+a2x2+…+a2010x2010,则a0+a2+a4+…+a2010被3除的余数是
- A.0
- B.1
- C.2
- D.不能确定
C
分析:分别给二项式中的x赋值1,-1,两式相加求出a0+a1+a2+…+a2010,将22009写成(3-1)2009,利用二项式定理求出其展开式,由展开式的形式判断出被3除的余数.
解答:令x=1得62010=a0+a1+a2+…+a2010
令x=-1得22010=a0-a1+a2-a3…+a2010
两式相加得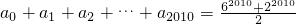 =22009•32010+22009
=22009•32010+22009
∵22009=(3-1)2009=C2009032009+C2009132008(-1)+…+C2009200831(-1)2008+C20092009(-1)2009
∴22009被3除的余数的是2
∴22009•32010+22009被3除的余数是2
即a0+a1+a2+…+a2010被3除的余数是2
故选C
点评:本题考查通过赋值法求展开式的系数和、利用二项式定理的展开式求余数问题.
分析:分别给二项式中的x赋值1,-1,两式相加求出a0+a1+a2+…+a2010,将22009写成(3-1)2009,利用二项式定理求出其展开式,由展开式的形式判断出被3除的余数.
解答:令x=1得62010=a0+a1+a2+…+a2010
令x=-1得22010=a0-a1+a2-a3…+a2010
两式相加得
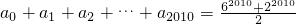 =22009•32010+22009
=22009•32010+22009∵22009=(3-1)2009=C2009032009+C2009132008(-1)+…+C2009200831(-1)2008+C20092009(-1)2009
∴22009被3除的余数的是2
∴22009•32010+22009被3除的余数是2
即a0+a1+a2+…+a2010被3除的余数是2
故选C
点评:本题考查通过赋值法求展开式的系数和、利用二项式定理的展开式求余数问题.

练习册系列答案
相关题目
(2x+4)2010=a0+a1x+a2x2+…+a2010x2010,则a0+a2+a4+…+a2010被3除的余数是( )
| A、0 | B、1 | C、2 | D、不能确定 |