题目内容
若对?x∈R,kx2-kx-1<0恒成立,则k的取值范围是
- A.-4≤k≤0
- B.-4≤k<0
- C.-4<k≤0
- D.-4<k<0
C
分析:由不等式可看到二次项系数有参数,故需要分两种情况k=0和k≠0研究.
解答:(1)当k=0时,不等式kx2-kx-1<0即为-1<0,成立,
故k=0满足题意;
(2)当k≠0时,因为对?x∈R,kx2-kx-1<0恒成立,
所以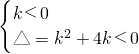 ,
,
所以-4<k<0.
综上所述(-4,0].
故选C.
点评:本题考察恒成立问题解决方法及分类讨论,属中档题.
分析:由不等式可看到二次项系数有参数,故需要分两种情况k=0和k≠0研究.
解答:(1)当k=0时,不等式kx2-kx-1<0即为-1<0,成立,
故k=0满足题意;
(2)当k≠0时,因为对?x∈R,kx2-kx-1<0恒成立,
所以
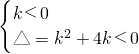 ,
,所以-4<k<0.
综上所述(-4,0].
故选C.
点评:本题考察恒成立问题解决方法及分类讨论,属中档题.

练习册系列答案
相关题目