题目内容
对于函数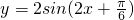 ,则下列结论正确的是
,则下列结论正确的是
- A.
 的图象关于点
的图象关于点 对称
对称 - B.
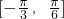 在区间
在区间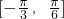 递增
递增 - C.
 的图象关于直线
的图象关于直线 对称
对称 - D.最小正周期是

B
分析:根据正弦函数的周期性和对称性、单调性,对各个选项进行判断,从而得出结论.
解答:由于点 不在函数
不在函数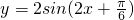 的图象上,故函数图象不关于点
的图象上,故函数图象不关于点 对称,故排除A.
对称,故排除A.
令 2kπ- ≤
≤ ≤2kπ+
≤2kπ+ ,k∈z,解得 kπ-
,k∈z,解得 kπ- ≤x≤kπ+
≤x≤kπ+ ,k∈z,故函数的增区间为
,k∈z,故函数的增区间为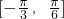 ,故B正确.
,故B正确.
当 时,函数值y=
时,函数值y= ,不是最值,故函数的图象不关于
,不是最值,故函数的图象不关于 对称,故排除C.
对称,故排除C.
由函数的解析式可得,最小正周期等于T= =π,故D不正确.
=π,故D不正确.
综上可得,只有B正确,
故选B.
点评:本题主要考查正弦函数的周期性和对称性、单调性,属于中档题.
分析:根据正弦函数的周期性和对称性、单调性,对各个选项进行判断,从而得出结论.
解答:由于点
 不在函数
不在函数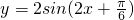 的图象上,故函数图象不关于点
的图象上,故函数图象不关于点 对称,故排除A.
对称,故排除A.令 2kπ-
 ≤
≤ ≤2kπ+
≤2kπ+ ,k∈z,解得 kπ-
,k∈z,解得 kπ- ≤x≤kπ+
≤x≤kπ+ ,k∈z,故函数的增区间为
,k∈z,故函数的增区间为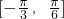 ,故B正确.
,故B正确.当
 时,函数值y=
时,函数值y= ,不是最值,故函数的图象不关于
,不是最值,故函数的图象不关于 对称,故排除C.
对称,故排除C.由函数的解析式可得,最小正周期等于T=
 =π,故D不正确.
=π,故D不正确.综上可得,只有B正确,
故选B.
点评:本题主要考查正弦函数的周期性和对称性、单调性,属于中档题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
(2007
江西师大附中模拟)设a<0,对于函数 ,则下列结论正确的是
,则下列结论正确的是
[
]|
A .有最大值而无最小值 |
B .有最小值而无最大值 |
|
C .有最大值且有最小值 |
D .既无最大值又无最小值 |
 ,则下列结论正确的是( )
,则下列结论正确的是( ) 的图象关于点
的图象关于点 对称
对称 在区间
在区间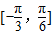 递增
递增 的图象关于直线
的图象关于直线 对称
对称
 ,有下列结论:①
,有下列结论:①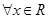 ,函数
,函数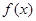 是偶函数;
②
是偶函数;
②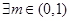 ,使得方程
,使得方程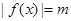 有两个不等实数根;
③
有两个不等实数根;
③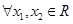 ,若
,若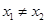 ,则一定有
,则一定有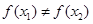 ;④
;④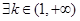 ,使得函数
,使得函数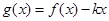 在
在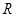 上有三个零点。
上有三个零点。